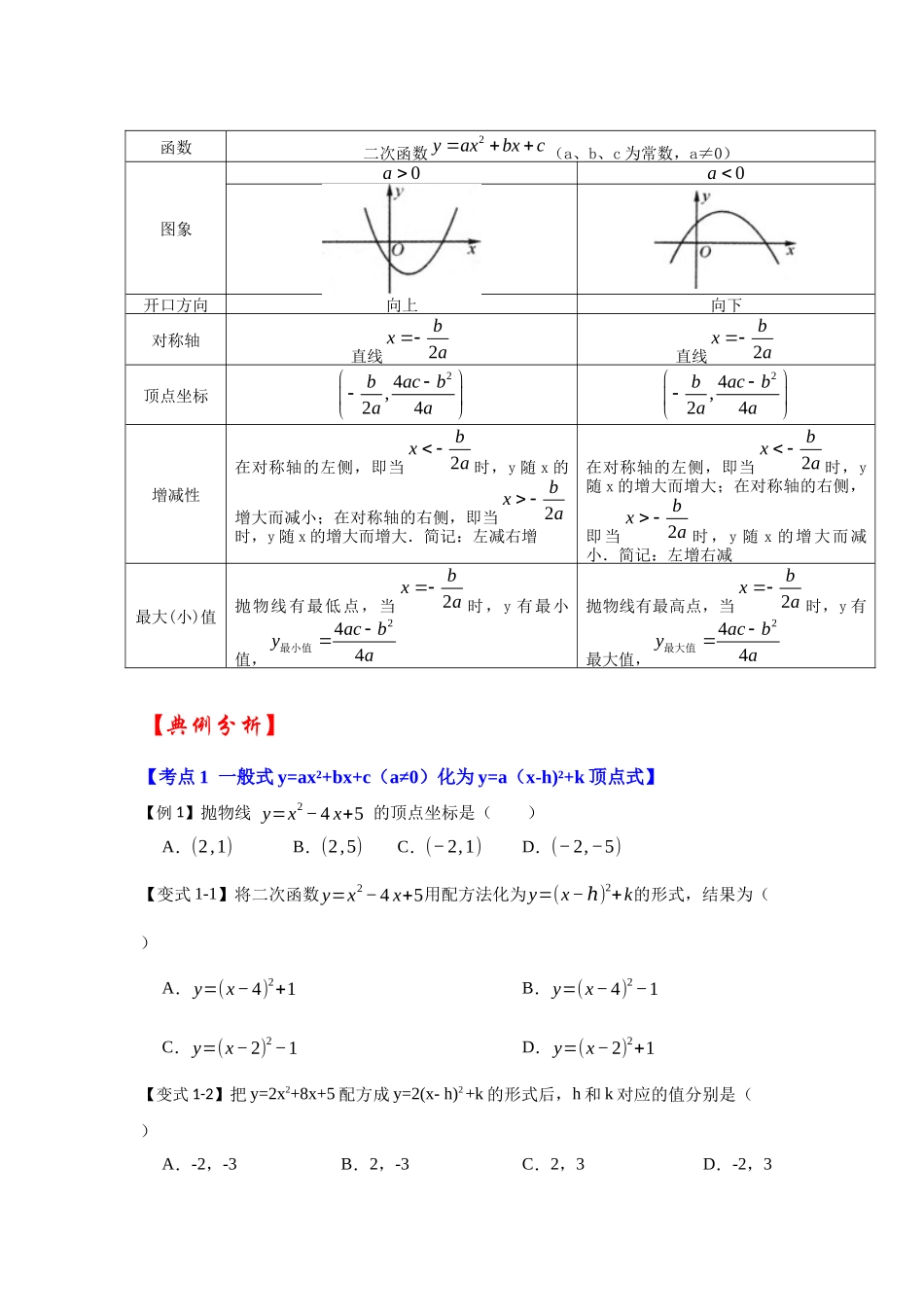
专题 22.1.5 二次函数 y=ax²+bx+c(a≠0)图像和性质(知识解读 1)【直击考点】【学习目标】1. 会 用 描 点 法 画 二 次 函 数2(0)yaxbxc a的 图 象 ; 会 用 配 方 法 将 二 次 函 数2yaxbxc的解析式写成2()ya xhk的形式;2. .通过图象能熟练地掌握二次函数2yaxbxc的性质;3. .经历探索2yaxbxc与2()ya xhk的图象及性质紧密联系的过程,能运用二次函数的图象和性质解决简单的实际问题,深刻理解数学建模思想以及数形结合的思想.【知识点梳理】考点 1 二次函数 y=ax²+bx+c(a≠0)与 y=a(x-h)²+k 之间的相互关系1. 顶点式化成一般式2. 从函数解析式2()ya xhk我们可以直接得到抛物线的顶点(h,k),所以我们称2()ya xhk为顶点式,将顶点式2()ya xhk去括号,合并同类项就可化成一般式2yaxbxc.3. 一般式化成顶点式2222222bbbbyaxbxca xxca xxcaaaa 22424bacba xaa.对照2()ya xhk,可知2bha,244acbka.∴ 抛物线2yaxbxc的对称轴是直线2bxa,顶点坐标是24,24bacbaa .考点 2 二次函数 y=ax²+bx+c(a≠0)图象的画法1.一般方法:列表、描点、连线;2.简易画法:五点定形法. 其步骤为: (1)先根据函数解析式,求出顶点坐标和对称轴,在直角坐标系中描出顶点 M,并用虚线画出对称轴. (2)求抛物线2yaxbxc与坐标轴的交点,当抛物线与 x 轴有两个交点时,描出这两个交点 A、B 及抛物线与 y 轴的交点 C,再找到点 C 关于对称轴的对称点 D,将A、B、C、D 及 M 这五个点按从左到右的顺序用平滑曲线连结起来.注意:当抛物线与 x 轴只有一个交点或无交点时,描出抛物线与 y 轴的交点 C 及对称点 D,由 C、M、D 三点可粗略地画出二次函数图象的草图;如果需要画出比较精确的图象,可再描出一对对称点 A、B,然后顺次用平滑曲线连结五点,画出二次函数的图象,考点 3 二次函数 y=ax²+bx+c(a≠0)的图像和性质【典例分析】【考点 1 一般式 y=ax²+bx+c(a≠0)化为 y=a(x-h)²+k 顶点式】【例 1】抛物线 y=x2−4 x+5 的顶点坐标是( ) A.(2,1) B.(2,5) C.(−2,1)D.(−2,−5)【变式 1-1】将二次函数y=x2−4 x+5用配方法化为y=(x...