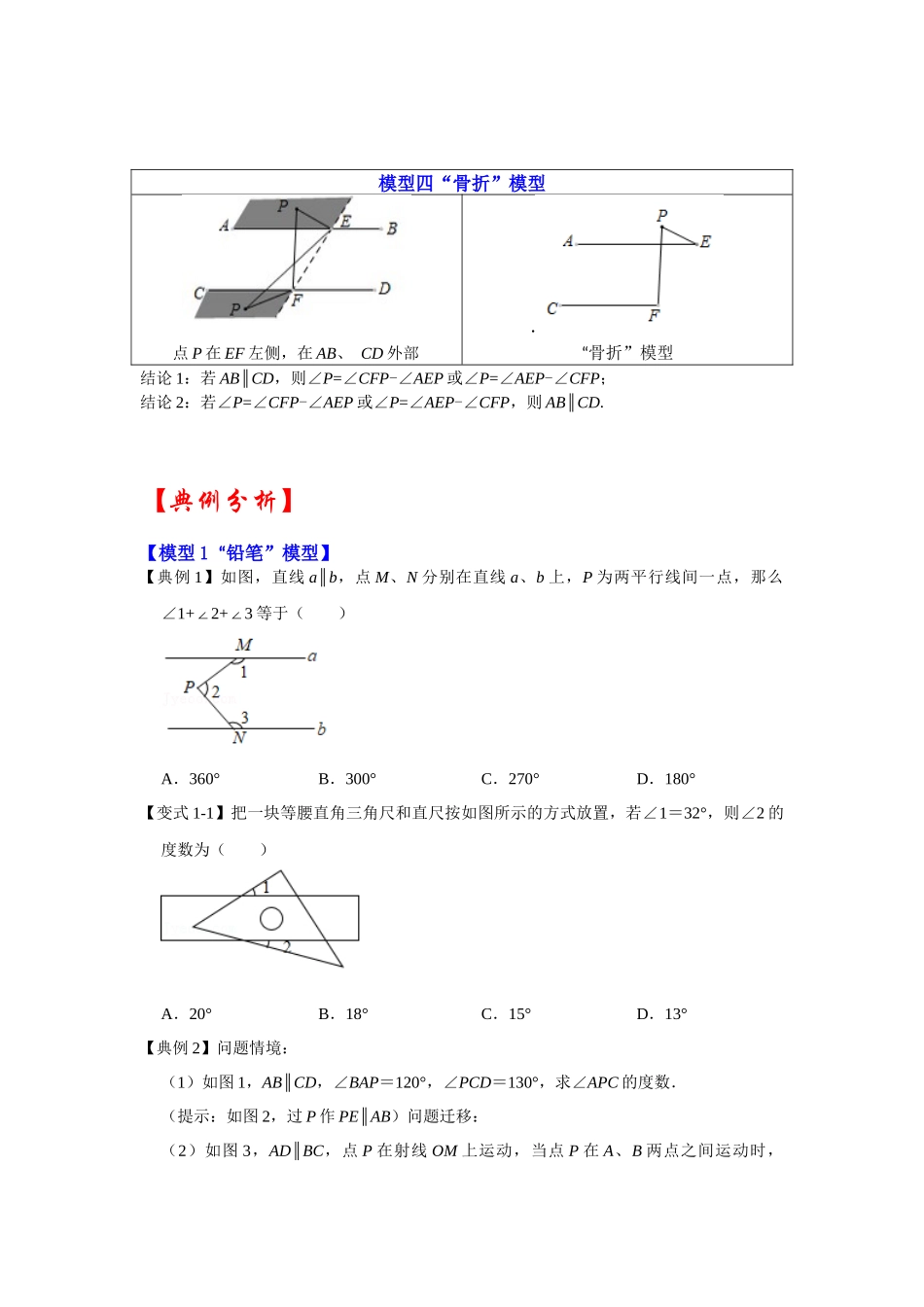
专题 03 平行线四大模型(知识解读)【专题说明】 历年中考考试中,有不少题目都考查了平行线的性质及应用,现汲取 四大模型,供同学们赏析,希望能到达指导学习之目的。【方法技巧】模型一“铅笔”模型点 P 在 EF 右侧,在 AB、 CD 内部“铅笔”模型结论 1:若 AB∥CD,则∠P+∠AEP+∠PFC=3 60° 结论 2:若∠P+∠AEP+∠PFC= 360°,则 AB∥CD. 模型二“猪蹄”模型(M 模型)点 P 在 EF 左侧,在 AB、 CD 内部“猪蹄”模型结论 1:若 AB∥CD,则∠P=∠AEP+∠CFP;结论 2:若∠P=∠AEP+∠CFP,则 AB∥CD.模型三“臭脚”模型点 P 在 EF 右侧,在 AB、 CD 外部“臭脚”模型结论 1:若 AB∥CD,则∠P=∠AEP-∠CFP 或∠P=∠CFP-∠AEP;结论 2:若∠P=∠AEP-∠CFP 或∠P=∠CFP-∠AEP,则 AB∥CD.模型四“骨折”模型点 P 在 EF 左侧,在 AB、 CD 外部·“骨折”模型结论 1:若 AB∥CD,则∠P=∠CFP-∠AEP 或∠P=∠AEP-∠CFP;结论 2:若∠P=∠CFP-∠AEP 或∠P=∠AEP-∠CFP,则 AB∥CD.【典例分析】【模型 1 “铅笔”模型】【典例 1】如图,直线 a∥b,点 M、N 分别在直线 a、b 上,P 为两平行线间一点,那么∠1+2+3∠∠ 等于( )A.360°B.300°C.270°D.180°【变式 1-1】把一块等腰直角三角尺和直尺按如图所示的方式放置,若∠1=32°,则∠2 的度数为( )A.20°B.18°C.15°D.13°【典例 2】问题情境:(1)如图 1,AB∥CD,∠BAP=120°,∠PCD=130°,求∠APC 的度数.(提示:如图 2,过 P 作 PE∥AB)问题迁移:(2)如图 3,AD∥BC,点 P 在射线 OM 上运动,当点 P 在 A、B 两点之间运动时,∠ADP=α,∠PCB=β,α、β、∠DPC 之间有何数量关系?请说明理由;(3)在(2)的条件下,如果点 P 在 A、B 两点外侧运动时(点 P 与点 A、B、O 三点不重合),请你直接写出 α、β、∠DPC 之间的数量关系.(提示:三角形内角和为180°)【变式 2-1】已知,AB∥CD,试解决下列问题:(1)如图 1,∠1+2∠ = ;(2)如图 2,∠1+2+3∠∠ = ;(3)如图 3,∠1+2+3+4∠∠∠ = ;(4)如图 4,试探究∠1+2+3+4+…+∠∠∠∠n= .【变式 2-2】如图,已知 BQ∥GE,AF∥DE,∠1=50°.(1)求∠AFG 的度数;(2)若 AQ 平分∠FAC,交 BC 于点 Q,且∠Q=15°,求∠ACB 的度数.【模型 2 “猪蹄”模型(M 模型)...