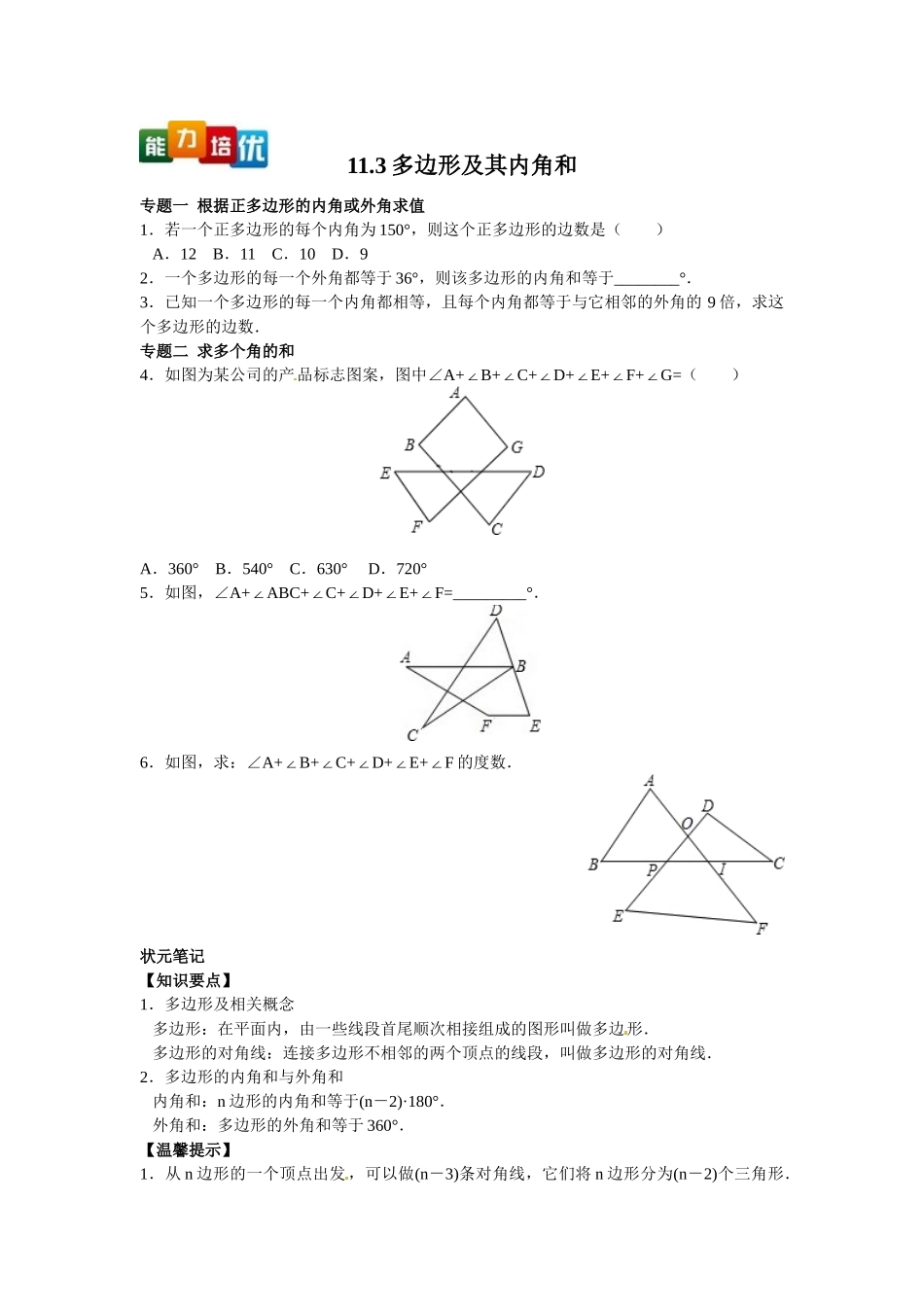
11.3 多边形及其内角和专题一 根据正多边形的内角或外角求值1.若一个正多边形的每个内角为 150°,则这个正多边形的边数是( ) A.12 B.11 C.10 D.92.一个多边形的每一个外角都等于 36°,则该多边形的内角和等于________°.3.已知一个多边形的每一个内角都相等,且每个内角都等于与它相邻的外角的 9 倍,求这个多边形的边数.专题二 求多个角的和4.如图为某公司的产品标志图案,图中∠A+B+C+D+E+F+G=∠∠∠∠∠∠( )A.360° B.540° C.630° D.720°5.如图,∠A+ABC+C+D+E+F=∠∠∠∠∠_________°.6.如图,求:∠A+B+C+D+E+F∠∠∠∠∠ 的度数.状元笔记【知识要点】1.多边形及相关概念 多边形:在平面内,由一些线段首尾顺次相接组成的图形叫做多边形. 多边形的对角线:连接多边形不相邻的两个顶点的线段,叫做多边形的对角线.2.多边形的内角和与外角和 内角和:n 边形的内角和等于(n-2)·180°. 外角和:多边形的外角和等于 360°.【温馨提示】1.从 n 边形的一个顶点出发 ,可以做(n-3)条对角线,它们将 n 边形分为(n-2)个三角形.对角线的条数与分成的三角形的个数不要弄错.2.多边形的外角和等于 360°,而不是 180°.【方法技巧】1.连接多边形的对角线,将多边形转化为多个三角形,将多边形问题转化为三角形问题来解决.2.多边形的内角和随边数的变化而变化,但外角和不变,都等于 360°,可利用多边形的外角和不变求多边形的边数等.参考答案:1 . A 解 析 : ∵ 每 个 内 角 为 150° , ∴ 每 个 外 角 等 于 30° . ∵ 多 边 形 的 外 角 和 是360°,360°÷30°=12,∴这个正多边形的边数为 12.故选 A.2.1440 解析:∵多边形的边数为 360°÷36°=10,多边形的内角为 180°-36°=144°,∴多边形的内角和等于 144°×10=1440°.3.解:设多边形的边数为 n,根据题意,得(n-2)·180°=9×360°,解得 n=20.所以这个多边形的边数为 20.4.B 解析:∵∠1=C+D∠∠ ,∠2=E+F∠∠ ,A+B+C+D+E+F+G∴∠∠∠∠∠∠∠ =A+B+1+2+G=540°∠∠∠∠∠.故选 B.5.360° 解析:在四边形 BEFG 中,EBG=C+D∵∠∠∠ ,BGF=A+ABC∠∠∠,A+ABC+C+D+E+F=EBG+BGF+E+F=360°∴∠∠∠∠∠∠∠∠∠∠.6.解:∵∠POA 是△OEF 的外角,∴∠POA=E+F∠∠ .同理:∠BPO=∠D+∠C.A+B+BPO+POA=360°∵∠∠∠∠,A+B+C+D+E+F=360°∴∠∠∠∠∠∠.