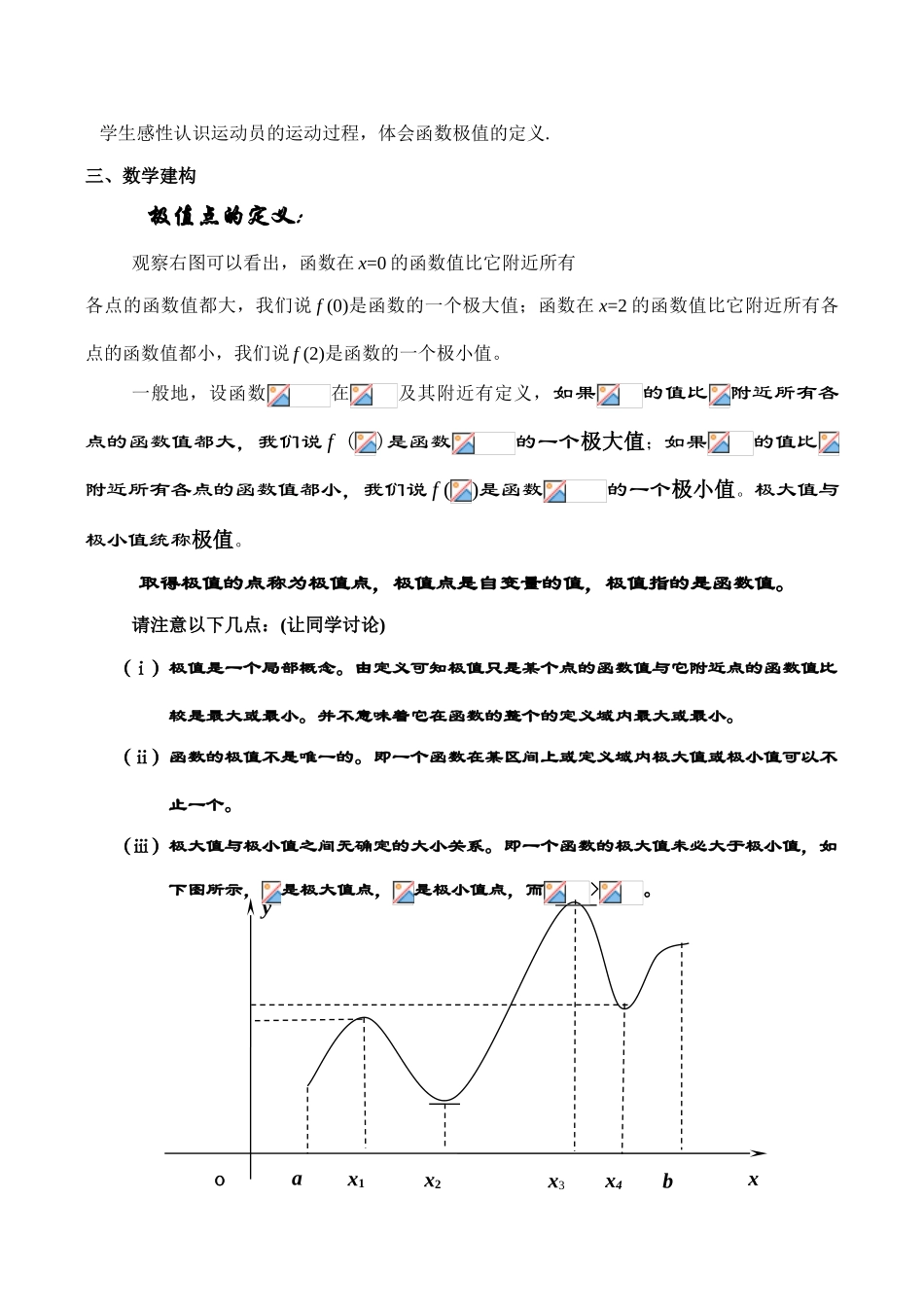
高一数学 函数极值点学案教学目标:(1)知识技能目标:① 了解函数极值的定义,会从几何图形直观理解函数的极值与其导数的关系,增强学生的数形结合意识,提升思维水平;② 掌握利用导数求可导函数的极值的一般方法;③ 了解可导函数极值点与=0 的逻辑关系;④ 培养学生运用导数的基本思想去分析和解决实际问题的能力.(2)过程与方法目标:培养学生观察→分析→探究→归纳得出数学概念和规律的学习能力。(3)情感与态度目标:培养学生层层深入、一丝不苟研究事物的科学精神;体会数学中的局部与整体的辨证关系.教学重点、难点:(1) 重点:掌握求可导函数的极值的一般方法. (2)难点:为函数极值点与=0 的逻辑关系.教学过程:一、问题情境 利用学生们熟悉的海边体育运动—冲浪,直观形象地引入函数极值的定义.观察下图中 P 点附近图像从左到右的变化趋势、P 点的函数值以及点 P 位置的特点函数图像在 P 点附近从左侧到右侧由“上升”变为“下降”(函数由单调递增变为单调递减),在 P 点附近,P 点的位置最高,函数值最大二、学生活动x02yoax1x2x34bxyP(x1,f(x1))y=f(x)Q(x2,f(x2))oax1x2x3x4bxy 学生感性认识运动员的运动过程,体会函数极值的定义.三、数学建构极值点的定义: 观察右图可以看出,函数在 x=0 的函数值比它附近所有各点的函数值都大,我们说 f (0)是函数的一个极大值;函数在 x=2 的函数值比它附近所有各点的函数值都小,我们说 f (2)是函数的一个极小值。一般地,设函数在及其附近有定义,如果的值比附近所有各点的函数值都大,我们说 f ()是函数的一个极大值;如果的值比附近所有各点的函数值都小,我们说 f ()是函数的一个极小值。极大值与极小值统称极值。取得极值的点称为极值点,极值点是自变量的值,极值指的是函数值。请注意以下几点:(让同学讨论)(ⅰ)极值是一个局部概念。由定义可知极值只是某个点的函数值与它附近点的函数值比较是最大或最小。并不意味着它在函数的整个的定义域内最大或最小。(ⅱ)函数的极值不是唯一的。即一个函数在某区间上或定义域内极大值或极小值可以不止一个。(ⅲ)极大值与极小值之间无确定的大小关系。即一个函数的极大值未必大于极小值,如下图所示,是极大值点,是极小值点,而>。oax0bxyoa x0bxy(ⅳ)函数的极值点一定出现在区间的内部,区间的端点不能成为极值点。而使函数取得最大值、最小值的点可能在区间的内部,也可能在区间的端点。极值点与导数...