（25-26学年）人教九年级上册学案24.2.2 第3课时 切线长定理及三角形的内切圆（训练附答案）VIP专享

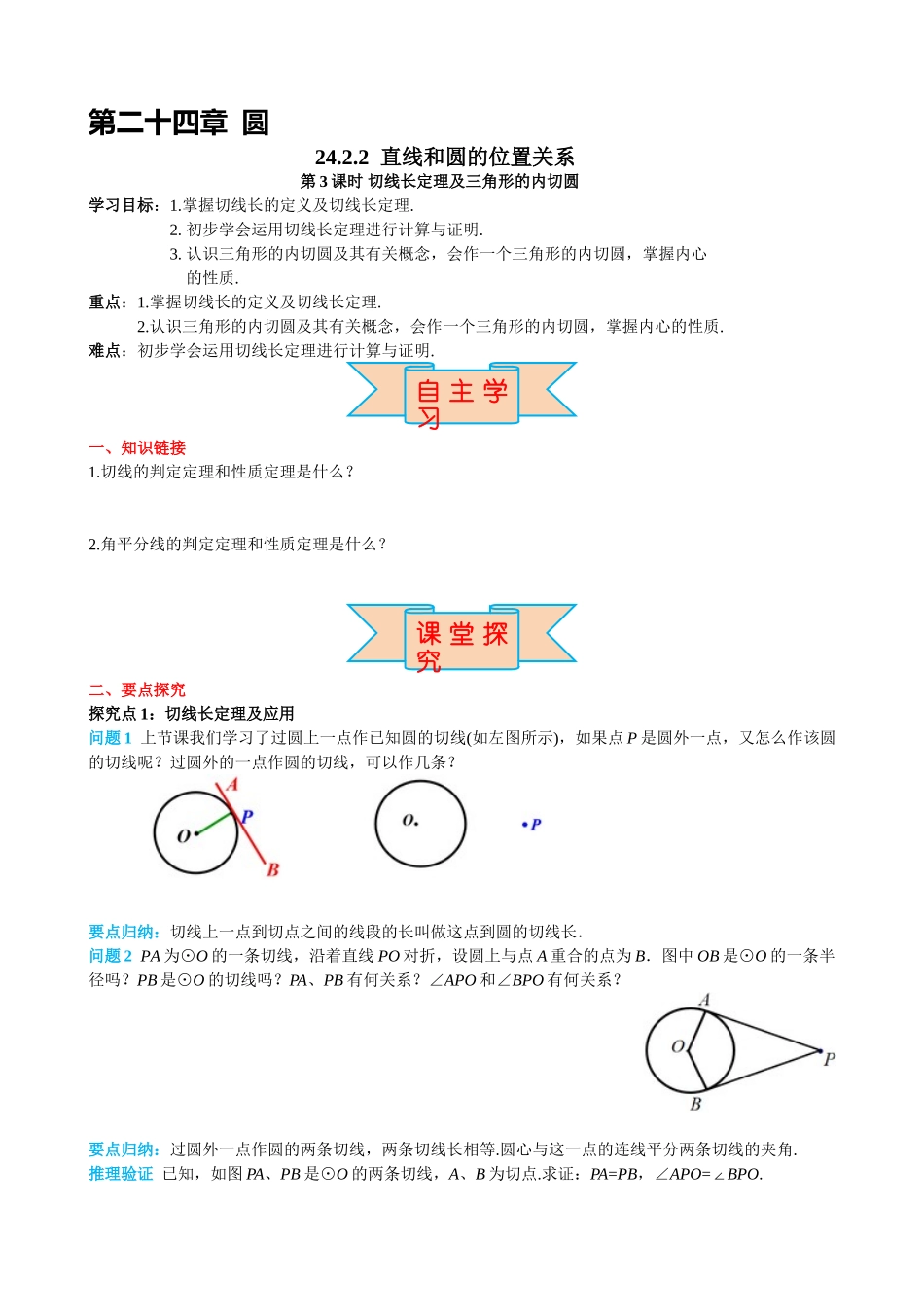
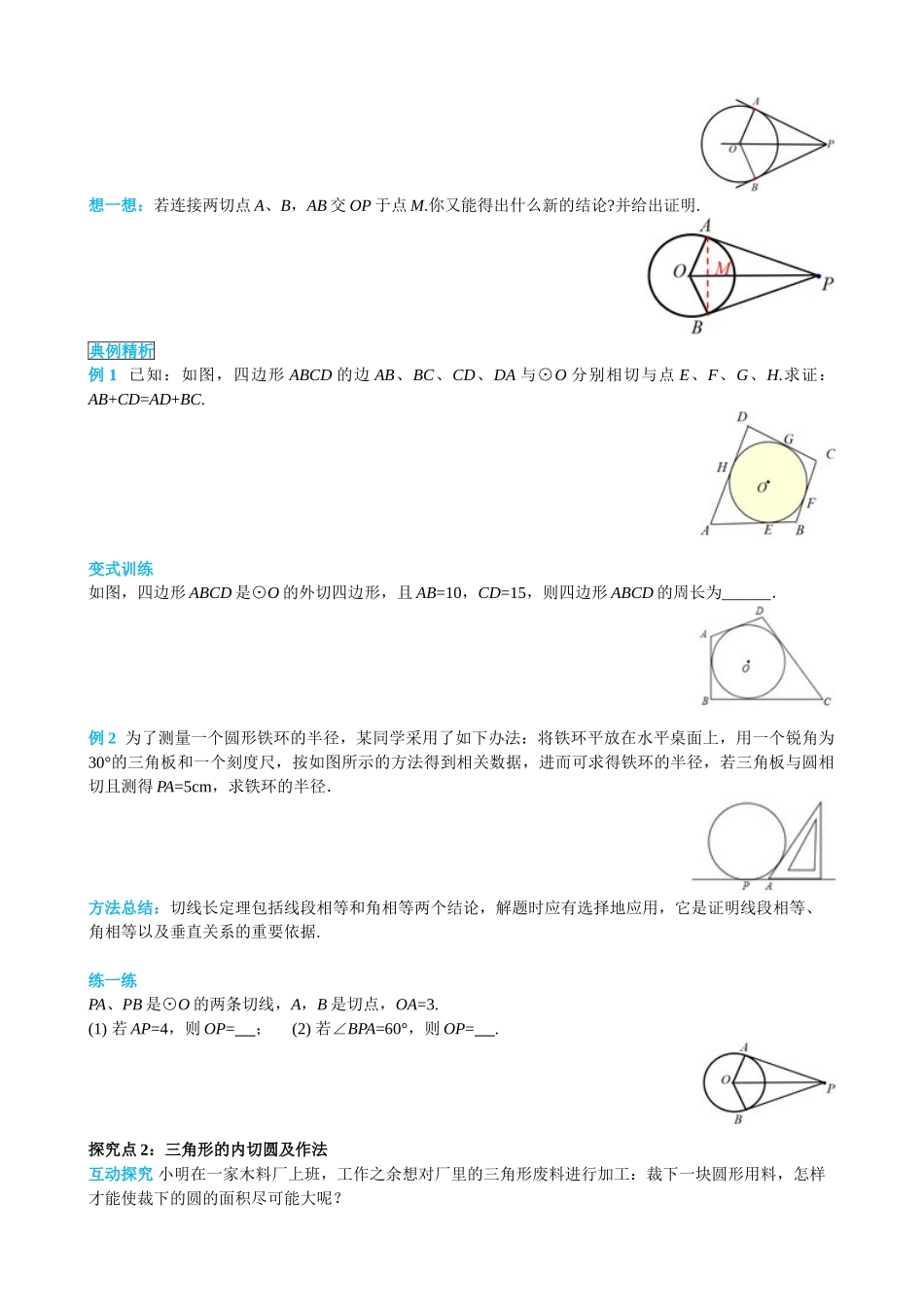
第二十四章 圆24.2.2 直线和圆的位置关系第 3 课时 切线长定理及三角形的内切圆学习目标：1.掌握切线长的定义及切线长定理.2. 初步学会运用切线长定理进行计算与证明.3. 认识三角形的内切圆及其有关概念，会作一个三角形的内切圆，掌握内心 的性质.重点：1.掌握切线长的定义及切线长定理.2.认识三角形的内切圆及其有关概念，会作一个三角形的内切圆，掌握内心的性质.难点：初步学会运用切线长定理进行计算与证明.一、知识链接1.切线的判定定理和性质定理是什么？ 2.角平分线的判定定理和性质定理是什么？二、要点探究探究点 1：切线长定理及应用问题 1 上节课我们学习了过圆上一点作已知圆的切线(如左图所示)，如果点 P 是圆外一点，又怎么作该圆的切线呢？过圆外的一点作圆的切线，可以作几条？ 要点归纳：切线上一点到切点之间的线段的长叫做这点到圆的切线长．问题 2 PA 为⊙O 的一条切线，沿着直线 PO 对折，设圆上与点 A 重合的点为 B．图中 OB 是⊙O 的一条半径吗？PB 是⊙O 的切线吗？PA、PB 有何关系？∠APO 和∠BPO 有何关系？要点归纳：过圆外一点作圆的两条切线，两条切线长相等.圆心与这一点的连线平分两条切线的夹角.推理验证 已知，如图 PA、PB 是⊙O 的两条切线，A、B 为切点.求证：PA=PB，∠APO=∠BPO.自 主 学习课 堂 探究想一想：若连接两切点 A、B，AB 交 OP 于点 M.你又能得出什么新的结论?并给出证明.典例精析例 1 已知：如图，四边形 ABCD 的边 AB、BC、CD、DA 与⊙O 分别相切与点 E、F、G、H.求证：AB+CD=AD+BC.变式训练如图，四边形 ABCD 是⊙O 的外切四边形，且 AB=10，CD=15，则四边形 ABCD 的周长为______．例 2 为了测量一个圆形铁环的半径，某同学采用了如下办法：将铁环平放在水平桌面上，用一个锐角为30°的三角板和一个刻度尺，按如图所示的方法得到相关数据，进而可求得铁环的半径，若三角板与圆相切且测得 PA=5cm，求铁环的半径．方法总结：切线长定理包括线段相等和角相等两个结论，解题时应有选择地应用，它是证明线段相等、角相等以及垂直关系的重要依据.练一练PA、PB 是⊙O 的两条切线，A，B 是切点，OA=3.(1) 若 AP=4，则 OP= ； (2) 若∠BPA=60°，则 OP= .探究点 2：三角形的内切圆及作法互动探究 小明在一家木料厂上班，工作之余想对厂里的三角形废料进行加工：裁下一块圆形用料，怎样才能使裁下的圆的面积尽可能大呢？问...