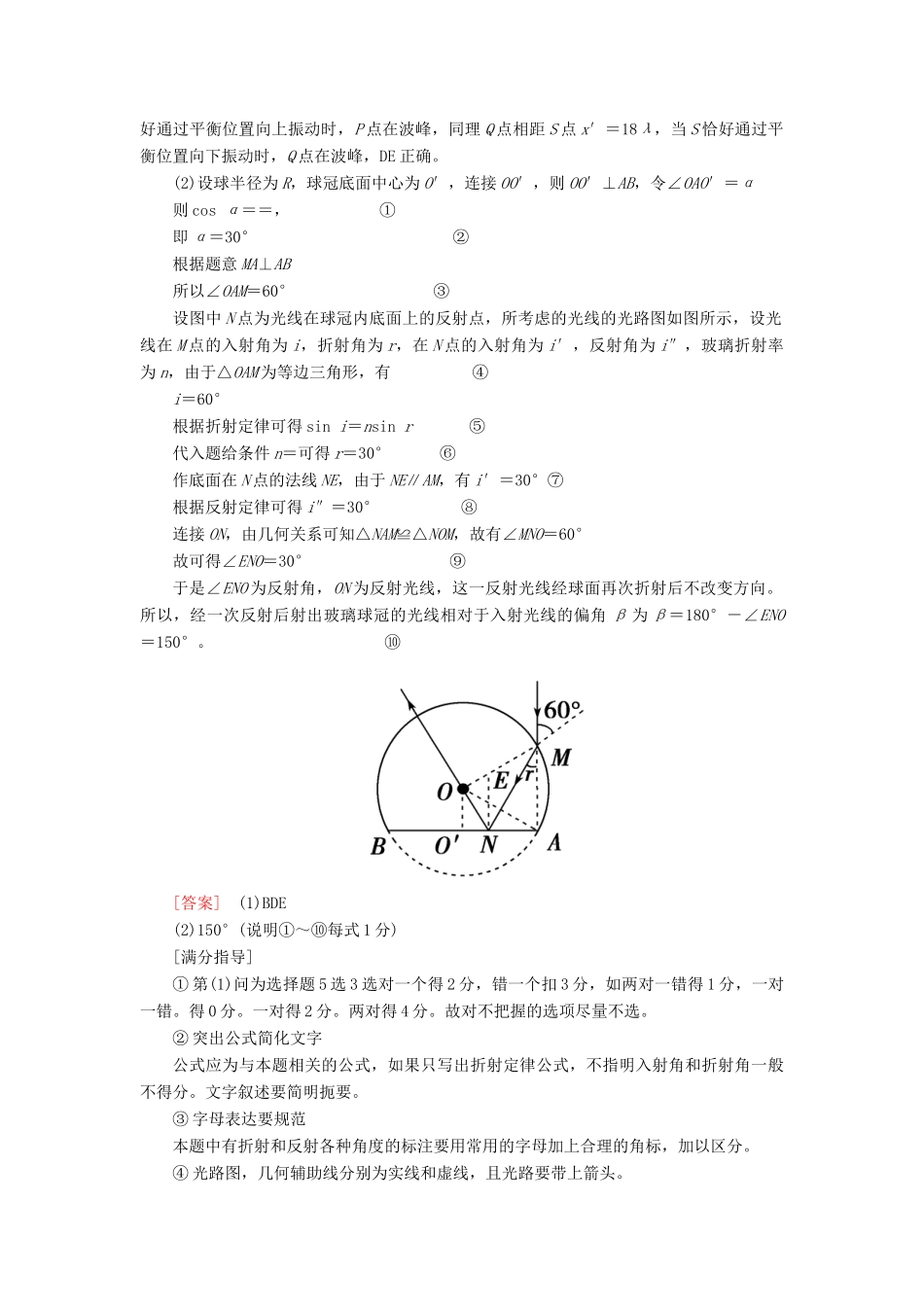
考点 2 机械振动与机械波 光学规范答题与满分指导机械与波、光学问题【典例】 (1)由波源 S 形成的简谐横波在均匀介质中向左、右传播。波源振动的频率为 20 Hz,波速为 16 m/s。已知介质中 P、Q 两质点位于波源 S 的两侧,且 P、Q 和 S 的平衡位置在一条直线上,P、Q 的平衡位置到 S 的平衡位置之间的距离分别为 15.8 m、14.6 m,P、Q 开始振动后,下列判断正确的是A.P、Q 两质点运动的方向始终相同B.P、Q 两质点运动的方向始终相反C.当 S 恰好通过平衡位置时,P、Q 两点也正好通过平衡位置D.当 S 恰好通过平衡位置向上运动时,P 在波峰E.当 S 恰好通过平衡位置向下运动时,Q 在波峰(2)如图 8-21,玻璃球冠的折射率为,其底面镀银,底面的半径是球半径的倍;在过球心 O 且垂直于底面的平面(纸面)内,有一与底面垂直的光线射到玻璃球冠上的 M 点,该光线的延长线恰好过底面边缘上的 A 点。求该光线从球面射出的方向相对于其初始入射方向的偏角。图 8-21[审题探究]1.通读题干,挖掘信息。①(1)中振源频率 f,波速 ν 已知。可求波长、知道两点到根源距离可判断 P、Q 两点的振动情况。②(2)中玻璃球冠的形状是关键点与底边长与半径关系,可求由 M 点入射光线的入射角。③ 由折射定律可求折射光线的方向,在底边的反射点。2.构建情景还原模型。①(1)问中两点在振源的两侧与两点在振源一侧完全相同,可以按 PQ 在振源一侧处理。②(2)问中玻璃球冠 M 点为入射点,球面可以用过 M 点的切面,来计算入射角和折射角,其法线为球心与 M 的连线。③ 由几何知识可知连线 BM 过球心为 O、△BMA 为直角三角形,∠ABM=30°[解析] (1)根据题意信息可得 T=s=0.05 s,v=16 m/s,故波长为 λ=vT=0.8 m,找 P 点关于 S 点的对称点 P′,根据对称性可知 P′和 P 的振动情况完全相同,P′、Q两点相距 Δx=λ=λ,为半波长的整数倍,所以两点为反相点,故 P′、Q 两点振动方向始终相反,即 P、Q 两点振动方向始终相反,A 错误 B 正确;P 点距离 S 点 x=19λ,当 S 恰好通过平衡位置向上振动时,P 点在波峰,同理 Q 点相距 S 点 x′=18λ,当 S 恰好通过平衡位置向下振动时,Q 点在波峰,DE 正确。(2)设球半径为 R,球冠底面中心为 O′,连接 OO′,则 OO′⊥AB,令∠OAO′=α则 cos α==, ①即 α=30° ②根据题意 MA⊥AB所以...