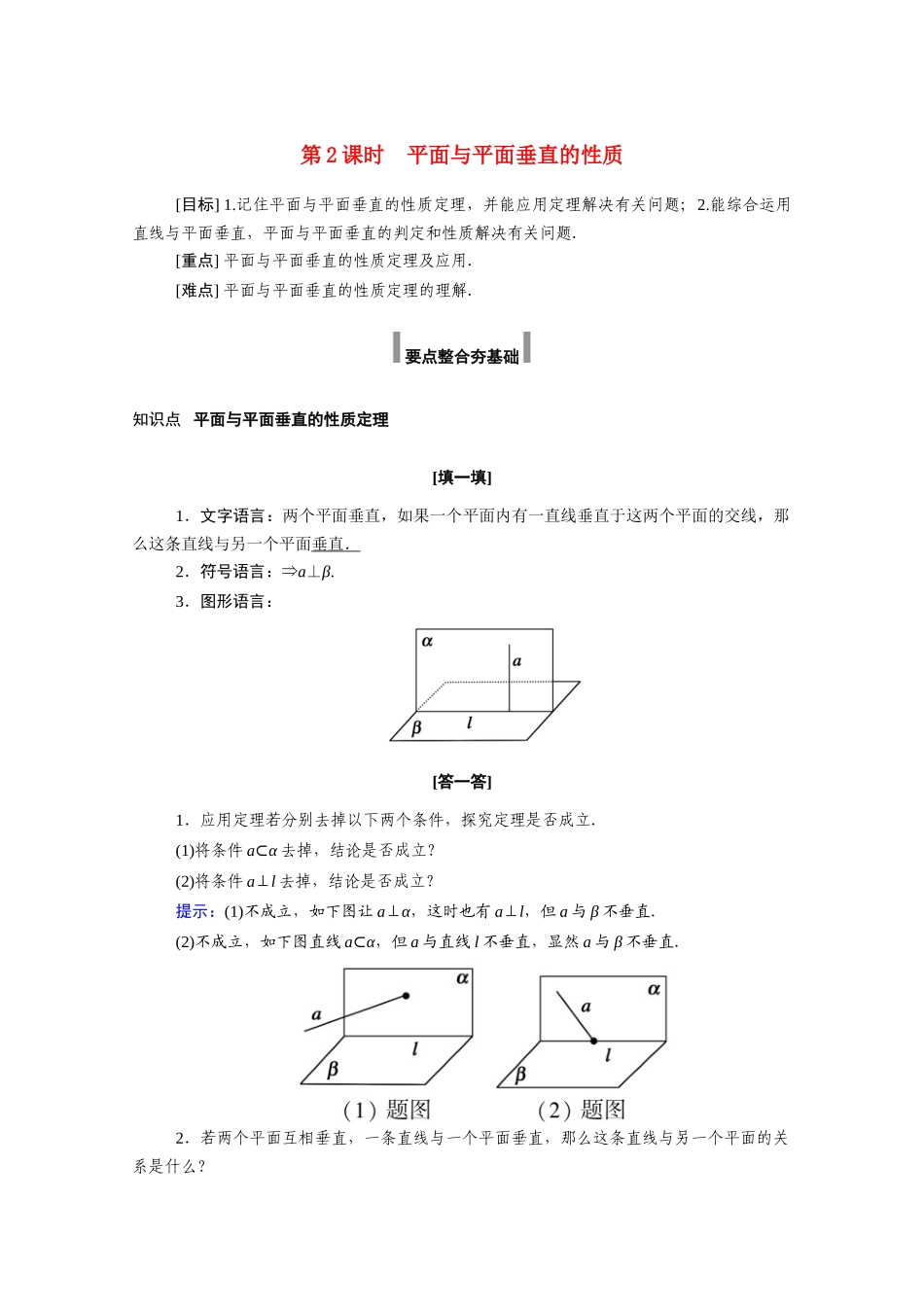
第 2 课时 平面与平面垂直的性质[目标] 1.记住平面与平面垂直的性质定理,并能应用定理解决有关问题;2.能综合运用直线与平面垂直,平面与平面垂直的判定和性质解决有关问题.[重点] 平面与平面垂直的性质定理及应用.[难点] 平面与平面垂直的性质定理的理解. 要点整合夯基础 知识点 平面与平面垂直的性质定理[填一填]1.文字语言:两个平面垂直,如果一个平面内有一直线垂直于这两个平面的交线,那么这条直线与另一个平面垂直.2.符号语言:⇒a⊥β.3.图形语言:[答一答]1.应用定理若分别去掉以下两个条件,探究定理是否成立.(1)将条件 a⊂α 去掉,结论是否成立?(2)将条件 a⊥l 去掉,结论是否成立?提示:(1)不成立,如下图让 a⊥α,这时也有 a⊥l,但 a 与 β 不垂直.(2)不成立,如下图直线 a⊂α,但 a 与直线 l 不垂直,显然 a 与 β 不垂直.2.若两个平面互相垂直,一条直线与一个平面垂直,那么这条直线与另一个平面的关系是什么?提示:若 α⊥β,l⊥α,在 β 内作 a 与 α,β 的交线垂直,则 a⊥α,∴a∥l.∴l∥β 或 l⊂β,即直线 l 与平面 β 平行或在平面 β 内. 典例讲练破题型 类型一 面面垂直性质定理的应用[例 1] 如图所示,P 是四边形 ABCD 所在平面外的一点,四边形 ABCD 是∠DAB=60°的菱形,侧面 PAD 为正三角形,其所在平面垂直于底面 ABCD.若 G 为 AD 边的中点,求证:BG⊥平面 PAD.[分析] 解答本题可先由面面垂直依据面面垂直的性质定理得线面垂直.[证明] 连接 BD, 四边形 ABCD 是菱形且∠DAB=60°,∴△ABD 是正三角形. G 是 AD 的中点,∴BG⊥AD.又平面 PAD⊥平面 ABCD,平面 PAD∩平面 ABCD=AD,∴BG⊥平面 PAD.证明线面垂直,一种方法是利用线面垂直的判定定理,另一种方法是利用面面垂直的性质定理,本题已知面面垂直,故可考虑面面垂直的性质定理.利用面面垂直的性质定理,证明线面垂直的问题时,要注意以下三点:1两个平面垂直;2直线必须在其中一个平面内;3直线必须垂直于它们的交线.[变式训练 1] 如图,在四棱锥 PABCD 中,平面 PAB⊥平面 ABCD,BC∥平面PAD,∠PBC=90°,∠PBA≠90°.求证:(1)AD∥平面 PBC;(2)平面 PBC⊥平面 PAB.证明:(1)因为 BC∥平面 PAD,而 BC⊂平面 ABCD,平面 ABCD∩平面 PAD=AD,所以 BC∥AD.因为 AD⊄平面 PBC,BC⊂平面 PBC,所以 AD∥...