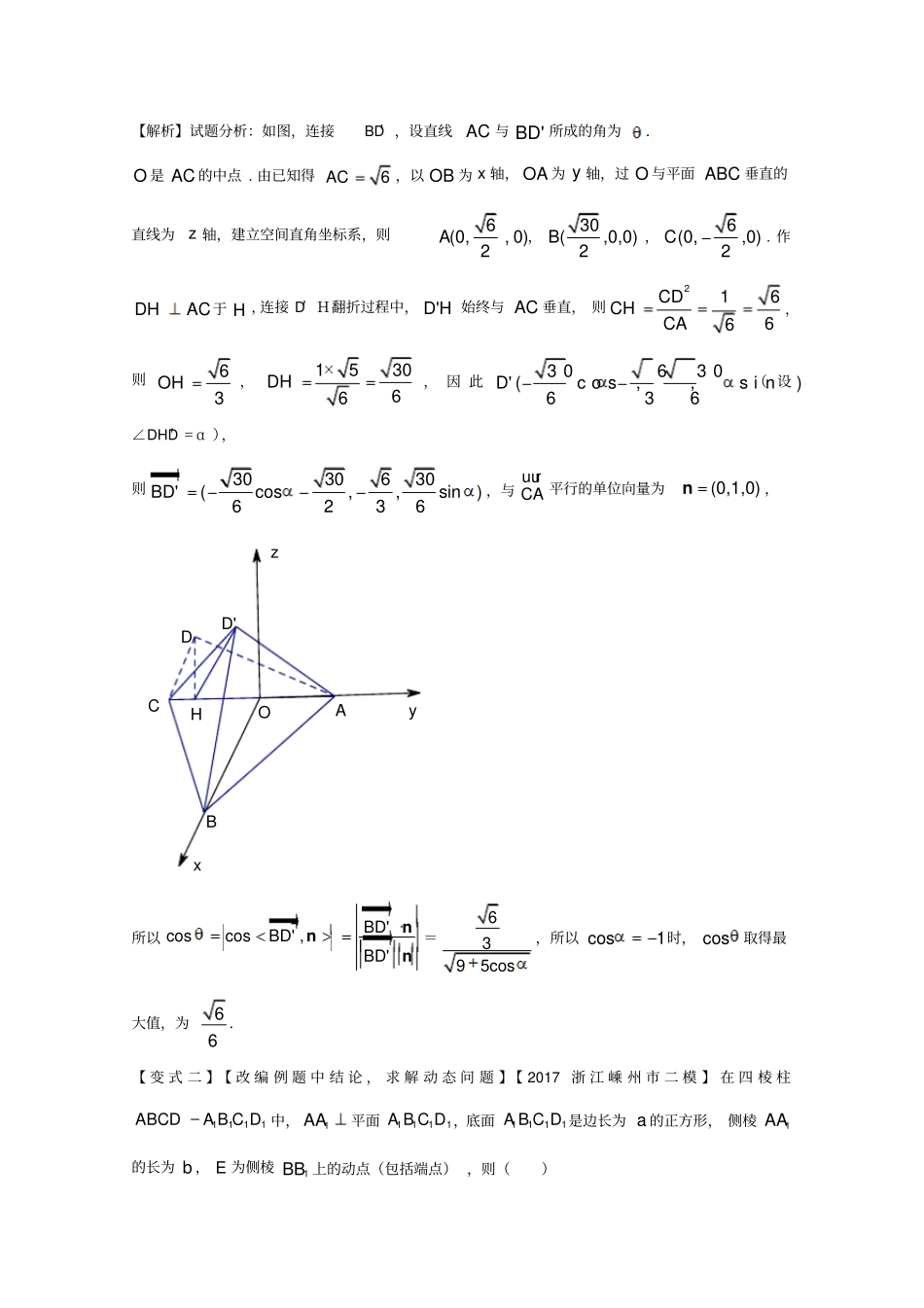
典型高考数学试题解读与变式2018版考点29:异面直线所成的角【考纲要求】1.能用向量方法解决直线与直线、直线与平面、平面与平面的夹角的计算问题.2.了解向量方法在研究立体几何问题中的应用.【命题规律】异面直线的知识是高考的热点问题,选择、填空、解答题都有可能进行考查.预计2018年的高考对本知识的考查空间向量的应用,仍然是以简单几何体为载体解决线线问题.【典型高考试题变式】(一)空间直线与直线夹角的问题例1.【2017全国3卷(理)】a,b为空间中两条互相垂直的直线,等腰直角三角形ABC的直角边AC所在直线与a,b都垂直,斜边AB以直线AC为旋转轴旋转,有下列结论:①当直线AB与a成60角时,AB与b成30角;②当直线AB与a成60角时,AB与b成60角;③直线AB与a所称角的最小值为45;④直线AB与a所称角的最小值为60;其中正确的是________.(填写所有正确结论的编号)【答案】②③【解析】由题意知,a,b,AC三条直线两两相互垂直,画出图形如图.不妨设图中所示正方体边长为1,故1AC,2AB,边AB以直线AC为旋转轴旋转,则A点保持不变,B点的运动轨迹是以C为圆心,1为半径的圆.以C为坐标原点,以CD为x轴正方向,CB为y轴正方向,CA为z轴正方向建立空间直角坐标系.则(1,0,0)D,(0,0,1)A,直线a的方向单位向量(0,1,0)a,1a.B点起始坐标为(0,1,0),直线b的方向单位向量(1,0,0)b,1b.设B点在运动过程中的坐标cos,sin,0B,其中为BC与CD的夹角,[0,2π).那么'AB在运动过程中的向量(cos,sin,1)AB,2AB.当AB与a夹角为60时,即π3,12sin2cos2cos2322.因为22cossin1,所以2cos2.所以21coscos22.因为π0,2.所以π=3,此时AB与b夹角为60.所以②正确,①错误.故填②③.【方法技巧归纳】求空间两条直线的夹角,可以先考察两条直线是否异面垂直,若垂直,则化为线面垂直问题或用平移法转化为共面垂直,结合勾股定理加以证明.一般情形,可通过平移后通过解斜三角形求两条异面直线所成的角.【变式1】【改编例题中条件,求两直线的夹角】【2016浙江(文)】如图,已知平面四边形ABCD,AB=BC=3,CD=1,AD=5,∠ADC=90°.沿直线AC将△ACD翻折成△ACD',直线AC与BD'所成角的余弦的最大值是______.【答案】66【解析】试题分析:如图,连接BD′,设直线AC与BD'所成的角为.O是AC的中点.由已知得6AC,以OB为x轴,OA为y轴,过O与平面ABC垂直的直线为z轴,建立空间直角坐标系,则6(0,,0)2A,30(,0,0)2B,6(0,,0)2C.作DHAC于H,连接D′H翻折过程中,D'H始终与AC垂直,则21666CDCHCA,则63OH,153066DH,因此30630(cos,,sin)636D'(设∠DHD′=α),则3030630(cos,,sin)6236BD',与CAuur平行的单位向量为(0,1,0)n,HD'DCBAzyxO所以coscos,BD'nBD'BD'nn=6395cos,所以cos1时,cos取得最大值,为66.【变式二】【改编例题中结论,求解动态问题】【2017浙江嵊州市二模】在四棱柱1111ABCDABCD中,1AA平面1111ABCD,底面1111ABCD是边长为a的正方形,侧棱1AA的长为b,E为侧棱1BB上的动点(包括端点),则()A.对任意的a,b,存在点E,使得11ECDBB.当且仅当ab时,存在点E,使得11ECDBC.当且仅当ba时,存在点E,使得11ECDBD.当且仅当ba时,存在点E,使得11ECDB【答案】C(二)异面直线的夹角例2.【2017全国2卷(理)】已知直三棱柱111ABCABC中,120ABC,2AB,11BCCC,则异面直线1AB与1BC所成角的余弦值为().A.32B.155C.105D.33【答案】C【解析】M,N,P分别为AB,1BB,11BC中点,则1AB,1BC夹角为MN和NP夹角或其补角(异面线所成角为π02,),可知11522MNAB,11222NPBC,作BC中点Q,则可知PQM△为直角三角形.1PQ,12MQACABC△中,2222cosACABBCABBCABC14122172,7AC则72MQ,则MQP△中,22112MPMQPQ,则PMN△中,222cos2MNNPPMPNMMHNP222521122210552222.又异面线所成角为π02,,则余弦值为105.故选C.【方法技巧归纳】1.利用向量法求异面直线所成角的步骤2.注意向量法求异面直线所成角与向量夹角的区别,尤其是取值范围.【变式1】【改编题目条件和结论,利用向量法求解】【2017届东北师大附中、哈尔滨师大附中、辽宁省实验中学四模】已知正四棱锥PABCD中,2,,PAABEF分别是,PBPC的中点...