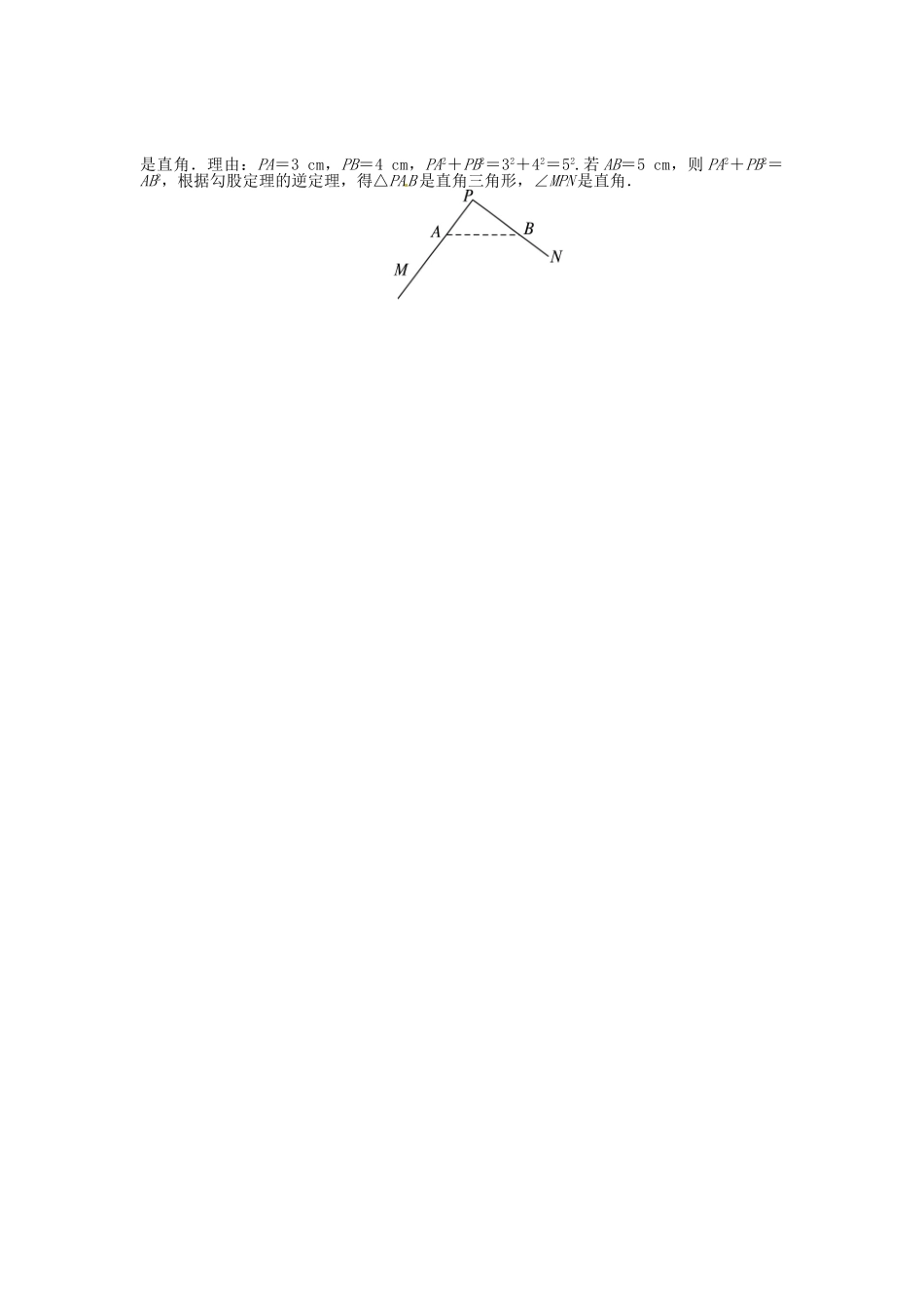
2.直角三角形的判定学前温故1.直角三角形有哪些性质?2.到目前为止,判定一个三角形是直角三角形,你有哪些方法?新课早知1.如果一个三角形的三边长a、b、c有关系:__________,那么这个三角形是直角三角形,这个结论就是“勾股定理的______”,其中____为斜边长.2.五根小木棒,其长度分别为7、15、20、24、25,现将它们摆成两个直角三角形,其中正确的是().答案:学前温故1.①有一个角是直角;②两锐角互余;③两直角边的平方和等于斜边的平方.2.①有一个角是直角的三角形是直角三角形;②有两个角的和是90°的三角形是直角三角形.新课早知1.a2+b2=c2逆定理c2.C选项A中,72+202=449≠242;选项B中,152+202=625≠242;选项C中,72+242=625=252,152+202=625=252;选项D中,152+242=801≠252,72+202=449≠252.所以只有选项C正确.1.怎样判定一个三角形是直角三角形【例1】已知△ABC的三边分别为2n、n2-1、n2+1(n为正整数),试判断△ABC的形状.分析:已知三边判断三角形的形状,通常考虑等腰或直角三角形,显然此处不是等腰三角形,可考虑直角三角形的判定方法.解:因为(n2+1)2=n4+2n2+1,(n2-1)2=n4-2n2+1,(2n)2=4n2,所以(n2+1)2=n4+2n2+1=(n4-2n2+1)+(4n2),即(n2+1)2=(n2-1)2+(2n)2.所以△ABC是直角三角形.点拨:判定一个三角形是直角三角形的常用方法:(1)利用定义.如果有一个角是直角,那么这个三角形是直角三角形.当题目中的条件与角有关时,常用这个方法.(2)利用勾股定理的逆定理.当已知三边的长或三边之间的关系时,常用此方法.在应用这个方法时,要注意找出哪条边是最长边,再就是验证两较短边的平方和是否等于最长边的平方.2.有关直角三角形判定的综合应用【例2】如图所示,在四边形ABCD中,∠D=90°,AB=12,CD=3,DA=4,BC=13,求四边形ABCD的面积.分析:要求四边形ABCD的面积,先把四边形ABCD分割成三角形,连结AC,△ADC是直角三角形,若△ACB也是直角三角形,问题就可解决.解:连结AC,因为∠ADC=90°,由勾股定理,得AC2=AD2+CD2,因此AC=5.而AC2+AB2=52+122=169=132=BC2,所以△ABC是直角三角形,且∠CAB=90°.S四边形ABCD=S△ADC+S△ABC=AD·CD+AC·AB=×4×3+×5×12=36.点拨:当题目中有直角三角形时,通常先运用勾股定理,求得相关线段的长度.1.小新和小明在玩猜数游戏,小新在手里写上三个数,然后告诉小明:我这手里的三个数是连续整数;小明说:三个连续的整数太多了,我猜不出来.小新说:我这三个数又恰好满足两个较小数的平方和等于最大数的平方.那么这三个数是().A.,,B.1,2,3C.2,3,4D.3,4,52.三角形的三边长分别为6、10、8,它的最短边上的高为().A.8B.6C.4.5D.2.43.从长分别为5、9、12、13、15的五条线段中取出三条,能构成直角三角形的取法有__________种,分别为__________.4.若△ABC的三边长a、b、c满足等式(a+b)2-c2=2ab,则△ABC的形状为__________.5.如果只给你一把带刻度的直尺,你是否能检验∠MPN是不是直角,简述你的作法.答案:1.D2.A3.25、12、13和9、12、154.直角三角形(a+b)2-c2=a2+2ab+b2-c2=2ab,∴a2+b2=c2.∴△ABC是直角三角形.5.解:作法:①在射线PM上量取PA=3cm,确定A点,在射线PN上量取PB=4cm,确定B点.②连结AB,得△PAB.③用刻度尺量取AB的长度,如果AB恰为5cm,则说明∠MPN是直角,否则∠MPN不是直角.理由:PA=3cm,PB=4cm,PA2+PB2=32+42=52.若AB=5cm,则PA2+PB2=AB2,根据勾股定理的逆定理,得△PAB是直角三角形,∠MPN是直角.