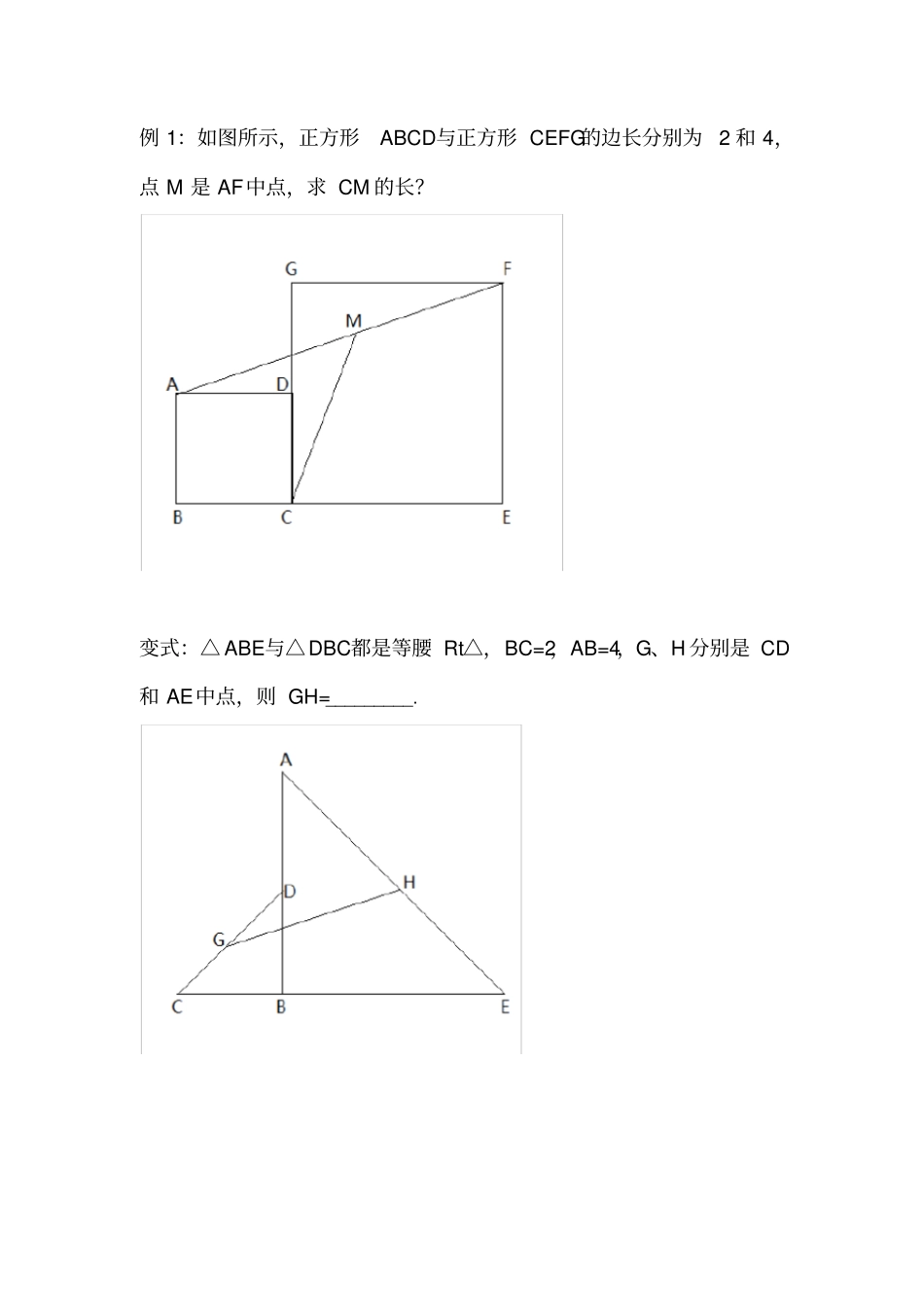
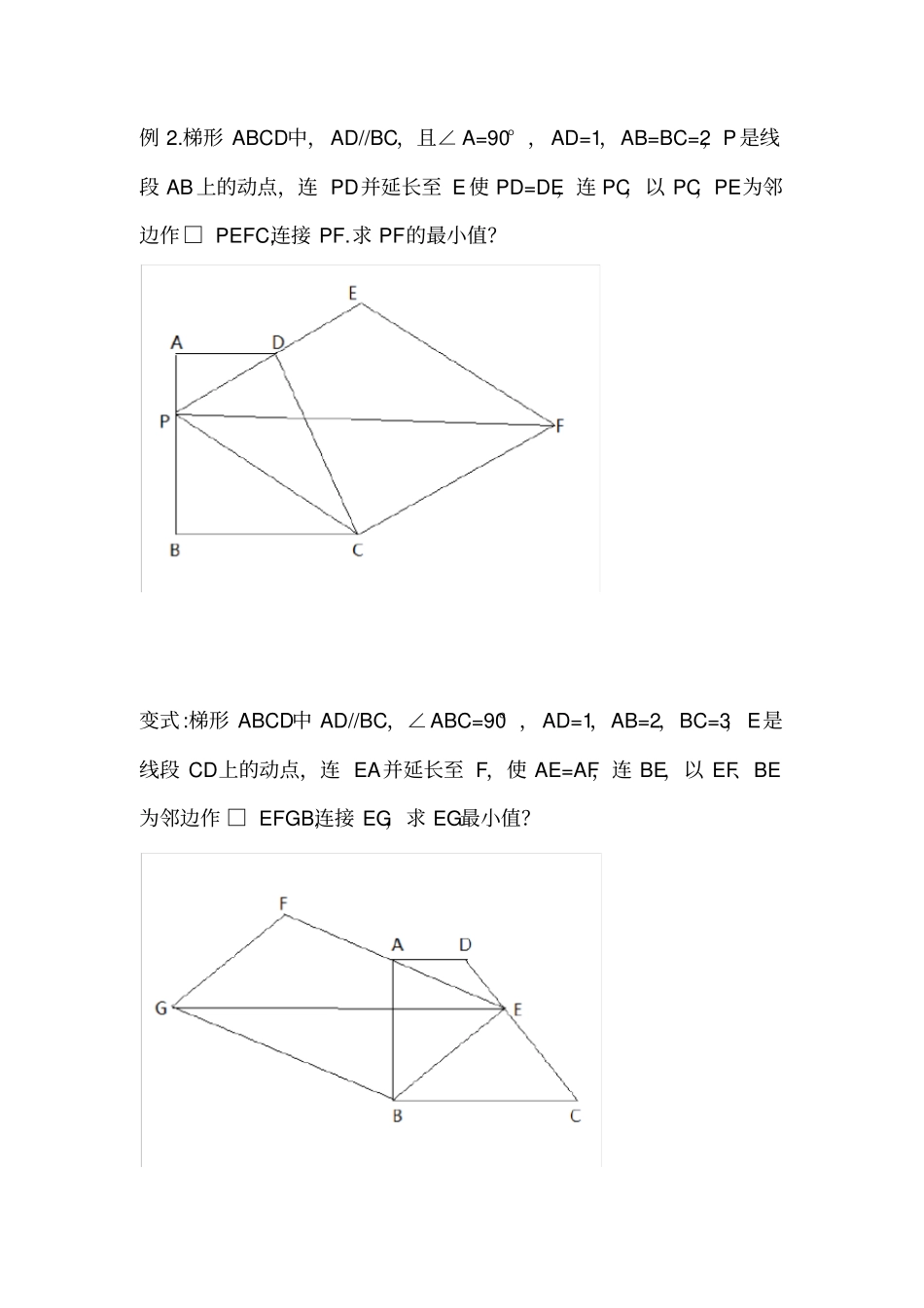
直线几何中的建系法在含有直角的几何图形(如直角三角形,直角梯形,矩形等)和等腰三角形、菱形这类有隐含直角的图形中,有关线段长度计算、线段比例关系计算还有特定的角度计算等几何问题,如果常规几何方式不好解决或过于繁杂,可通过构造平面直角坐标系的方式转化为函数或代数问题。这就是通常说的“建系法”。*建系法常用的知识点与结论1.k为定值,则直线与坐标轴的夹角为定值①|k|=1,与x轴、y轴夹角都为45°②|k|=,与x轴夹角60°,与y轴夹角30°③|k|=,与x轴夹角30°,与y轴夹角60°2.斜率公式A(x1,y1)和B(x2,y2)则kAB=3.直线点斜式方程过点P(x0,y0)且斜率为k的直线为y-y0=k(x-x0)4.恰当构造“K型”全等与相似求点的坐标5.定比分点公式点C(x0,y0)是线段AB上的一点,且=n,且A(x1,y1)和B(x2,y2)则x0=y0=例1:如图所示,正方形ABCD与正方形CEFG的边长分别为2和4,点M是AF中点,求CM的长?变式:△ABE与△DBC都是等腰Rt△,BC=2,AB=4,G、H分别是CD和AE中点,则GH=_________.例2.梯形ABCD中,AD//BC,且∠A=90°,AD=1,AB=BC=2,P是线段AB上的动点,连PD并延长至E使PD=DE,连PC,以PC,PE为邻边作□PEFC,连接PF.求PF的最小值?变式:梯形ABCD中AD//BC,∠ABC=90°,AD=1,AB=2,BC=3,E是线段CD上的动点,连EA并延长至F,使AE=AF,连BE,以EF、BE为邻边作□EFGB,连接EG,求EG最小值?例3.如图AB⊥CD,AB=BC=3,BD=2,E是线段AC上的动点,将BE绕点B逆时针旋转90°得BF,连接AF、BF.1.∠BAF是否为定值?2.求DF最小值?例4.Rt△ABC中,∠ACB=90°,=,D为BC中点,连接AD,作CE⊥AD,连接BE并延长交AC于F,求?变式:如图,矩形ABCD中=,G为AB中点,E、F为BC的三等分点,求GM:MN:NP:PC?建系法天天练1.矩形ABCD中AB=3,BC=4,E为BC边上的动点,以AE为边作正方形AEFG,求DF的最小值?2.已知OA=OB=4,∠AOB=90°,C为线段AB上的动点,以OC为直角边作等腰Rt△DOC,E为OB中点,求DE的最小值?3.正方形ABCD的边AB上任取一点E,作EF⊥AB交BD于F,取DF中点G,连接EG、CG,探究EG与CG的关系?4.如图所示,正方形ABCD和BEFG中,A,B,E在一条直线上,P为DF中点,探究PC与PG的关系?