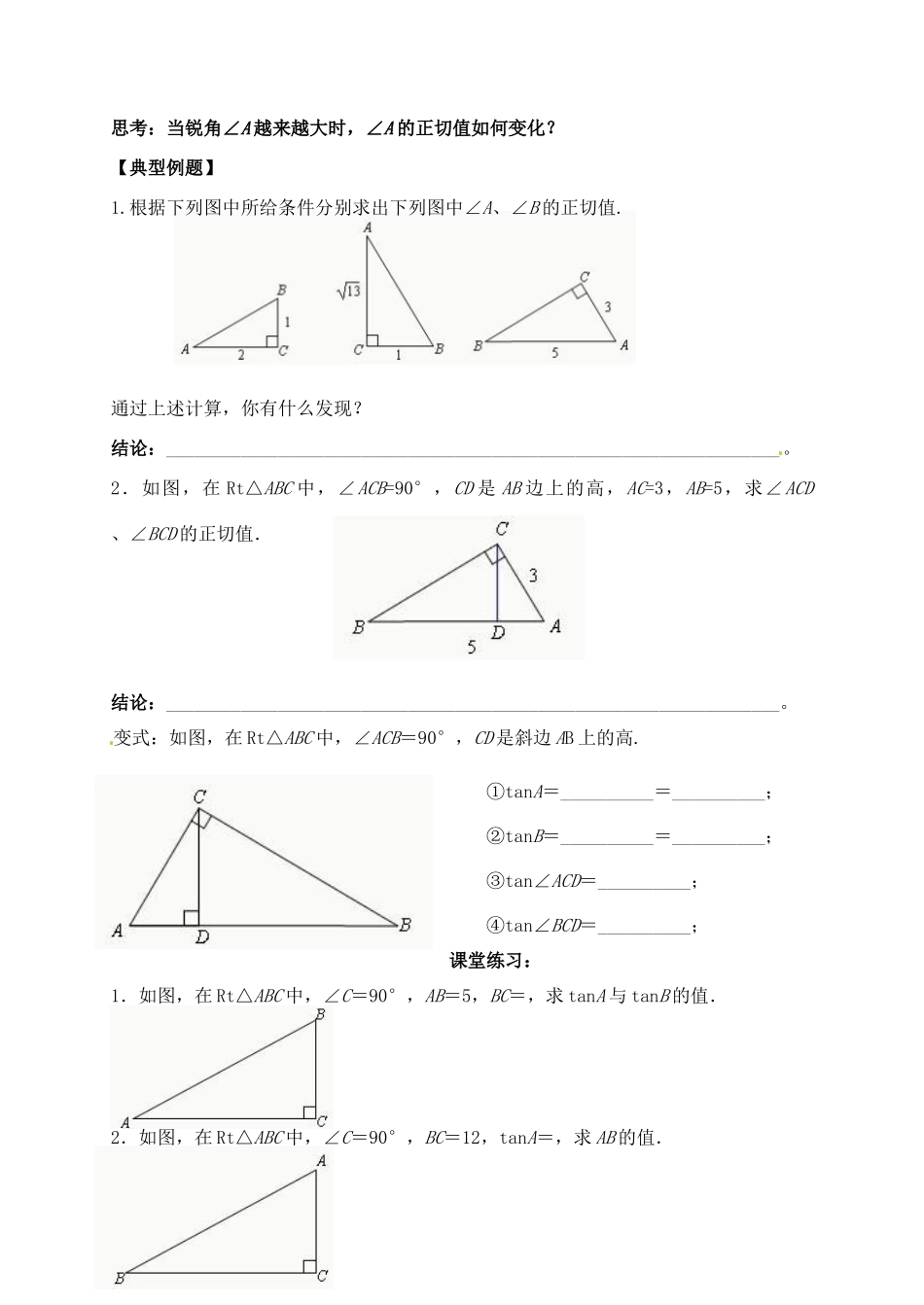
江苏省姜堰市蒋垛中学九年级数学《正切》教案人教版一.教学目标:知识与技能:理解并掌握正切的定义,会在直角三角形中求出某个锐角的正切值,能运用正切解决与直角三角形有关的简单问题。过程与方法:经历探索表示物体倾斜程度,形成正切的概念的过程,练就创造性解决问题的能力。二.教学重点:理解并掌握正切的含义,会在直角三角形中求出某个锐角的正切值。教学难点:求一个锐角的正切值的方法.三.教学过程导入:1.下列图中的两个台阶哪个更陡?你是怎么判断的?2.思考与探索:除了用∠A的大小来描述倾斜程度,我们还可以(1)可通过测量BC与AC的长度,再算出它们的比,来说明台阶的倾斜程度.(2)可通过测量B1C1与A1C1的长度,再算出它们的比,来说明台阶的倾斜程度.总结:一般地,如果锐角A的大小确定,我们可以作出无数个以A为一个顶点的直角三形(如图),那么图中:错误!未找到引用源。成立吗?为什么?结论:如果一个直角三角形的一个锐角的大小确定,那么这个锐角的对边与这个角的邻边的比值也确定。3.正切的定义:.思考:当锐角∠A越来越大时,∠A的正切值如何变化?【典型例题】1.根据下列图中所给条件分别求出下列图中∠A、∠B的正切值.通过上述计算,你有什么发现?结论:__________________________________________________________________。2.如图,在Rt△ABC中,∠ACB=90°,CD是AB边上的高,AC=3,AB=5,求∠ACD、∠BCD的正切值.结论:__________________________________________________________________。变式:如图,在Rt△ABC中,∠ACB=90°,CD是斜边AB上的高.①tanA=__________=__________;②tanB=__________=__________;③tan∠ACD=__________;④tan∠BCD=__________;课堂练习:1.如图,在Rt△ABC中,∠C=90°,AB=5,BC=,求tanA与tanB的值.2.如图,在Rt△ABC中,∠C=90°,BC=12,tanA=,求AB的值.BAC512BCA233.如图,在4×4的正方形网格中,tanα=__________.课时作业:1.根据下列图中所给条件分别求出下列图中∠A、∠B的正切值.2.如图,在直角△ABC中,∠ACB=90°,CD⊥AB于D,CD=3,AD=4,tanA=_______,tanB=______.3.如图,在正方形ABCD中,点E为AD的中点,连结EB,设∠EBA=α,则tanα=__________.4.在直角△ABC中,∠C=90°,BC=5,tanA=,求AB=_____.5.若锐角A,B满足tanA<tanB,则∠A,∠B的大小关系为__________________.6.如图,长为5m的梯子靠在一堵墙上,梯子的底端距离墙角3m,则梯子的倾斜角的正切值为__________.7.三角形在方格纸中的位置如图所示,则tanα的值是_______.8.如图,小明为了测量其所在位置A点到河对岸B点之间的距离,沿着与AB垂直的方向走了m米,到达点C,测得∠ACB=α,A3C2B第2题第3题第6题第7题那么AB等于___.9.如图,在Rt△ABC中,∠C=90°,AB=12,tanA=2,求AB的值.10.等腰三角形ABC的腰长AB,AC为5,底边长为6,求tanC.7.2正弦、余弦(1)一.教学目标:知识与技能:理解并掌握正弦、余弦的含义,会在直角三角形中求出某个锐角的正弦和余弦值。过程与方法:能用函数的观点理解正弦、余弦和正切。二.教学重点难点:教学重点:理解并掌握正弦、余弦的含义,会在直角三角形中求出某个锐角的正弦和余弦值。教学难点:在直角三角形中求出某个锐角的正弦和余弦值。三.教学过程问题1:如图,小明沿着某斜坡向上行走了13m后,他的相对位置升高了5m,如果他沿着该斜坡行走了20m,那么他的相对位置升高了多少?行走了am呢?问题2:在上述问题中,他在水平方向又分别前进了多远?思考:从上面的两个问题可以看出:当直角三角形的一个锐角的大小已确定时,它的对边与斜边的比值__________;它的邻边与斜边的比值___________.(根据是______________________.)正弦的定义:如图,在Rt△ABC中,∠C=90°,我们把锐角∠A的对边a与斜边c的比叫做∠A的______,记作________,即:sinA=________=________.余弦的定义:如图,在Rt△ABC中,∠C=90°,我们把锐角∠A的邻边b与斜边c的比叫做∠A的______,记作=_________,即:cosA=______=_____.(你能写出∠B的正弦、余弦的表达式吗?)...