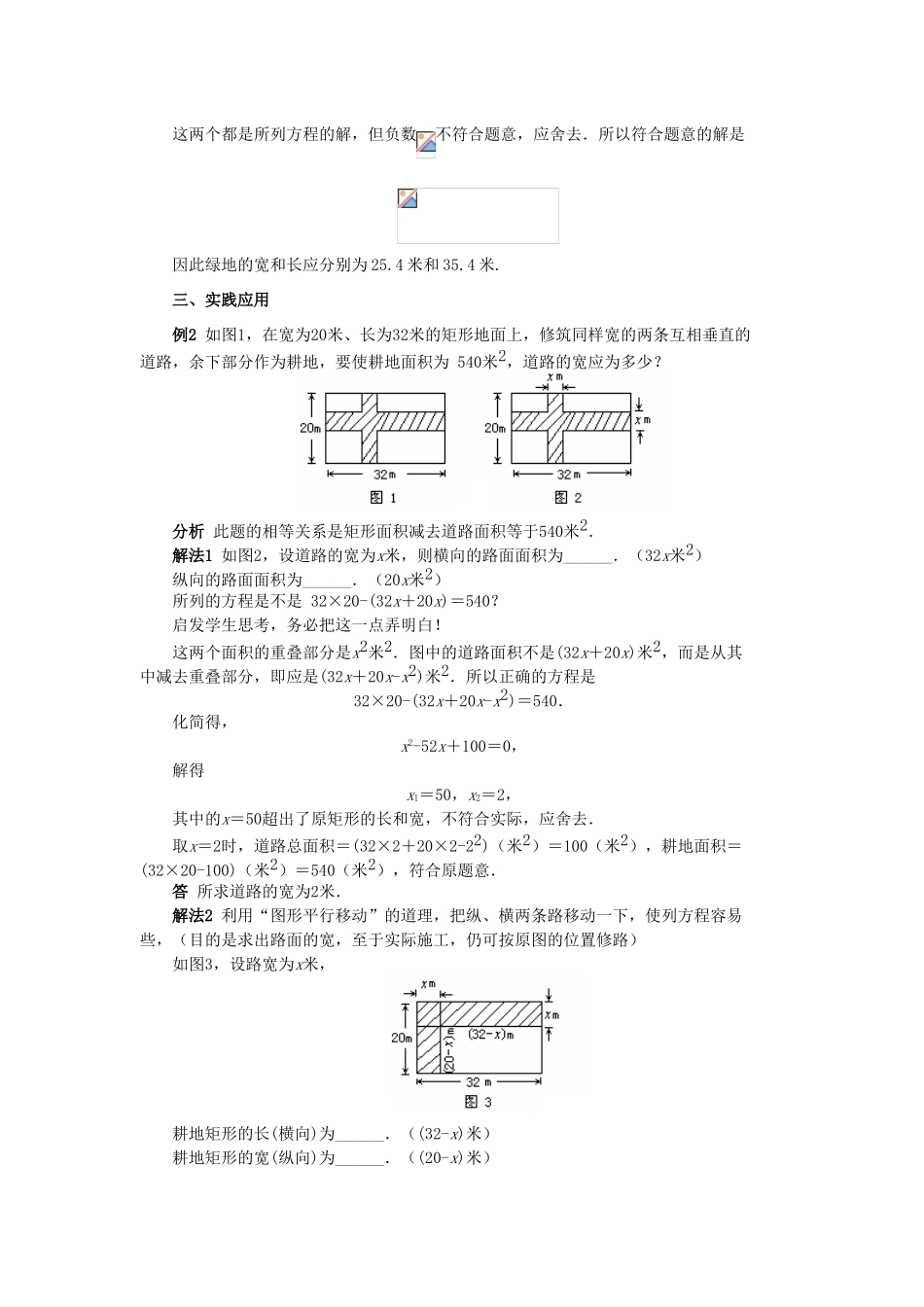
一元二次方程的解法(5)教学目标:知识技能目标1.使学生掌握列方程解应用题中写“关系式”及找相等关系列方程方法;2.使学生理解列方程实质在于会用含未知数的代数式表示题目里的关系式;3.采用对面积的割补、移动的方法,培养学生灵活运用的能力.过程性目标1.使学生会列方程解有关面积问题的应用题;2.进一步掌握解应用题的步骤和关键.情感态度目标1.通过例题使学生体会列方程的实质,培养灵活处理问题的能力;2.培养学生应用数学的意识.重点和难点:认真审题,分析题中数量关系,适当设未知数,寻找等量关系,列方程是重点也是难点.教学过程:一、创设情境1.写出本节课的课题:一元二次方程的应用.2.请同学们回忆并回答解一元一次方程应用题的一般步骤:第一步:弄清题意和题目中的已知数、未知数,用字母表示题目中的一个未知数;第二步:找出能够表示应用题全部含义的相等关系;第三步:根据这些相等关系列出需要的代数式,从而列出方程;第四步:解这个方程,求出未知数的值;第五步:检查求得的答数是否符合应用题的实际意义,写出答案(包括单位名称).3.解一元二次方程的应用题的步骤与解一元一次方程应用题的步骤一样.我们先来解决§22.1的问题1,然后总结一些规律或应注意事项.二、探究归纳例1绿苑小区住宅设计,准备在每两幢楼房之间,开辟面积为900平方米的一块长方形绿地,并且长比宽多10米,则绿地的长和宽各为多少?分析我们已经知道可以运用方程解决实际问题.现设长方形绿地宽为x米,不难列出方程:x(x+10)=900这两个都是所列方程的解,但负数不符合题意,应舍去.所以符合题意的解是因此绿地的宽和长应分别为25.4米和35.4米.三、实践应用例2如图1,在宽为20米、长为32米的矩形地面上,修筑同样宽的两条互相垂直的道路,余下部分作为耕地,要使耕地面积为540米2,道路的宽应为多少?分析此题的相等关系是矩形面积减去道路面积等于540米2.解法1如图2,设道路的宽为x米,则横向的路面面积为______.(32x米2)纵向的路面面积为______.(20x米2)所列的方程是不是32×20-(32x+20x)=540?启发学生思考,务必把这一点弄明白!这两个面积的重叠部分是x2米2.图中的道路面积不是(32x+20x)米2,而是从其中减去重叠部分,即应是(32x+20x-x2)米2.所以正确的方程是32×20-(32x+20x-x2)=540.化简得,x2-52x+100=0,解得x1=50,x2=2,其中的x=50超出了原矩形的长和宽,不符合实际,应舍去.取x=2时,道路总面积=(32×2+20×2-22)(米2)=100(米2),耕地面积=(32×20-100)(米2)=540(米2),符合原题意.答所求道路的宽为2米.解法2利用“图形平行移动”的道理,把纵、横两条路移动一下,使列方程容易些,(目的是求出路面的宽,至于实际施工,仍可按原图的位置修路)如图3,设路宽为x米,耕地矩形的长(横向)为______.((32-x)米)耕地矩形的宽(纵向)为______.((20-x)米)相等关系是:耕地长×耕地宽=540米2,即(32-x)(20-x)=540.化简得x2-52x+100=0,解得x1=50,x2=2.再往下的计算、格式书写与解法1相同.例3如图,一块长和宽分别为60厘米和40厘米的长方形铁皮,要在它的四角截去四个相等的小正方形,折成一个无盖的长方体水槽,使它的底面积为800平方米.求截去正方形的边长.分析设截去正方形的边长为x厘米后,关键在于列出底面(图示虚线部分)长和宽的代数式.结合图示和原有长方形的长和宽,不难得出这一代数式.解设截去正方形的边长为x厘米,根据题意,得(60-2x)(40-2x)=800.让同学解一下这个方程,并讨论它的解是否符合题意.学生练习:1.学生会准备举办一次摄影展览,在每张长和宽分别为18厘米和12厘米的长方形相片周围镶上一圈等宽的彩纸.经试验,彩纸面积为相片面积的三分之二时较美观,求镶上彩纸条的宽(精确到0.1厘米).2.竖直上抛物体的高度h和时间t符合关系式,其中重力加速度g以10米/秒2计算.爆竹点燃后以初速度v0=20米/秒上升,问经过多少时间爆竹离地15米?四、交流反思1.列方程解应用题的步骤是:(1)仔细了解题意及有关的事物的概念;(2)找题中给出的等量关系和隐含的等量关系;(3)选设未知数,并用含这个未...