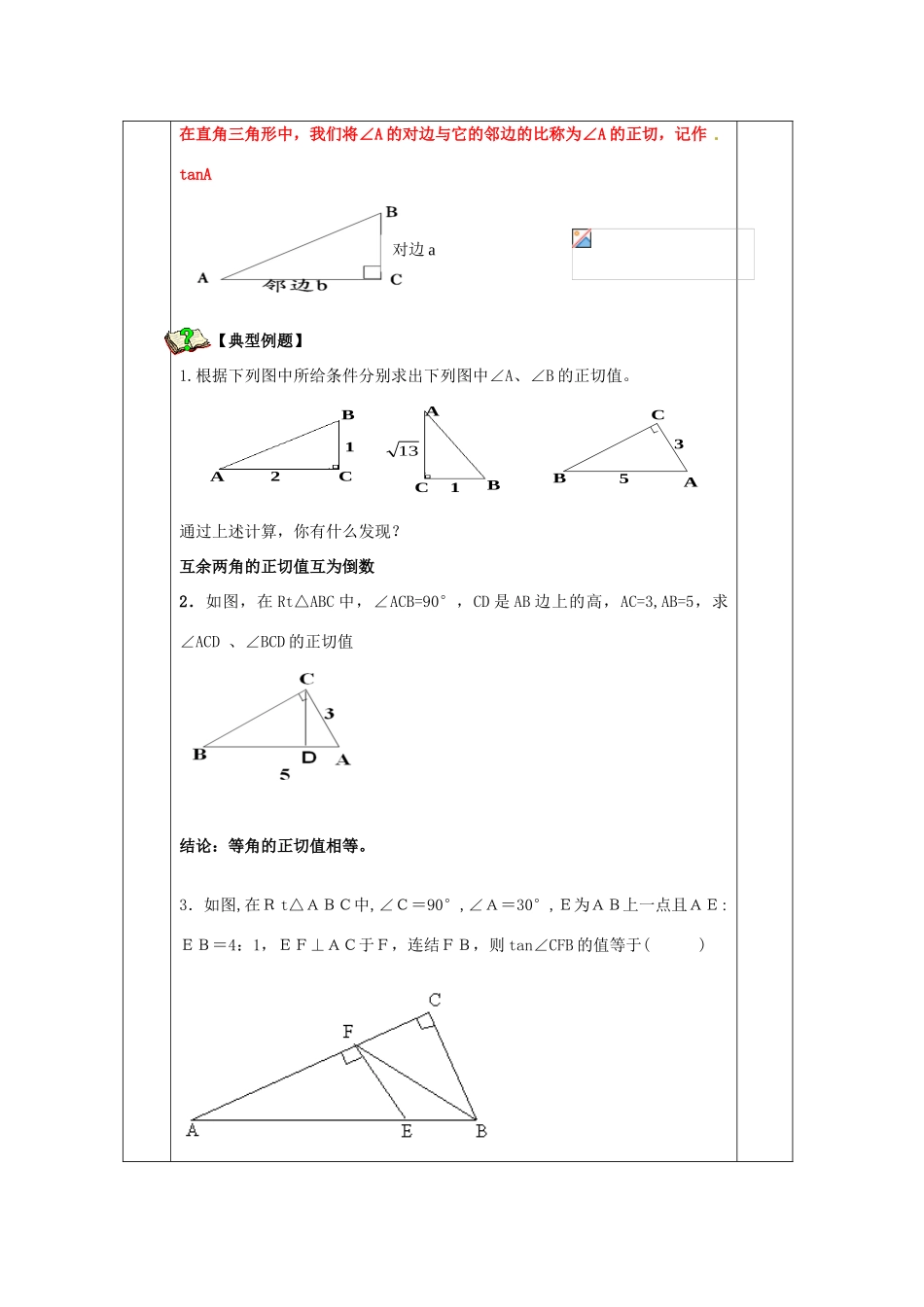
课题7.1正切教时1授课教学目标知识与技能:1学习目标:1、理解并掌握正切的含义,会在直角三角形中求出某个锐角的正切值。2、了解计算一个锐角的正切值的方法。个性化处理教学重点、难点计算一个锐角的正切值的方法教学手段PPT教学步骤及过程一、课前预习:如图,在Rt△ABC中,∠C=90°,AB=5,BC=,求tanA与tanB的值。【课前导入】1.下列图中的两个台阶哪个更陡?你是怎么判断的?2.思考与探索一除了用∠A的大小来描述倾斜程度,还可以用什么方法?(1)可通过测量BC与AC的长度,再算出它们的比,来说明台阶的倾斜程度.(2)可通过测量B1C1与A1C1的长度,再算出它们的比,来说明台阶的倾斜程度.总结:一般地,如果锐角A的大小确定,我们可以作出无数个以A为一个顶点的直角三形(如图),那么图中:成立吗?为什么?结论:如果一个直角三角形的一个锐角的大小确定,那么这个锐角的对边与这个角的邻边的比值也确定。3.正切的定义:ABC在直角三角形中,我们将∠A的对边与它的邻边的比称为∠A的正切,记作tanA【典型例题】1.根据下列图中所给条件分别求出下列图中∠A、∠B的正切值。BCA113A2C1BBAC35通过上述计算,你有什么发现?互余两角的正切值互为倒数2.如图,在Rt△ABC中,∠ACB=90°,CD是AB边上的高,AC=3,AB=5,求∠ACD、∠BCD的正切值结论:等角的正切值相等。3.如图,在Rt△ABC中,∠C=90°,∠A=30°,E为AB上一点且AE:EB=4:1,EF⊥AC于F,连结FB,则tan∠CFB的值等于()对边a4.在Rt△ABC中,∠CAB=90°,AD是∠CAB.的平分线,tanB=则CD∶DB=_______板书设计课题例题1例题2教学后让学生认识锐角的概念;在复杂的图形中灵活运用正切的知识解题是一个难点。