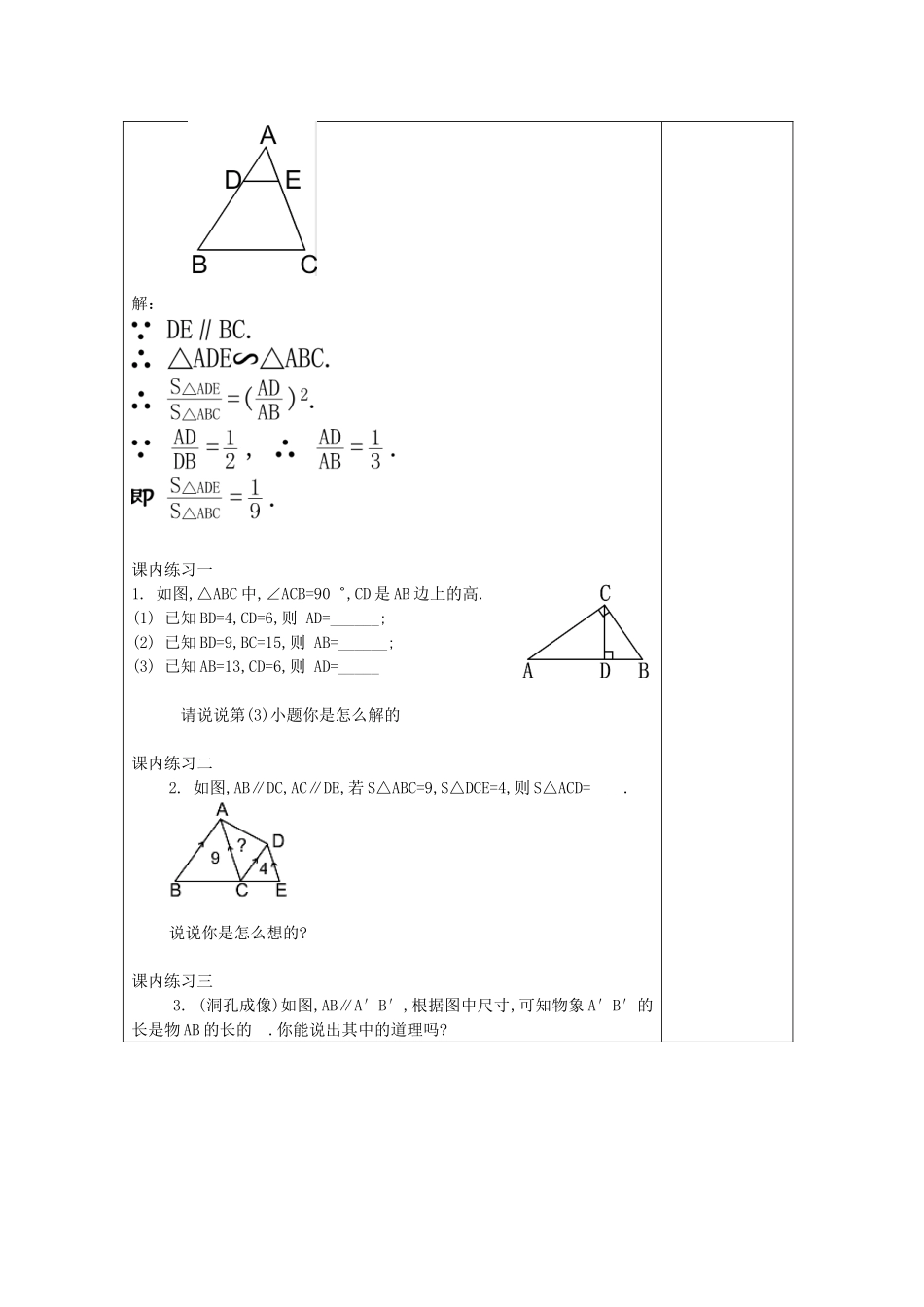
相似三角形的性质(相似三角形的性质(33))课题24.524.5相似三角形的性质(相似三角形的性质(33))课型练习课教学目标11.会用相似三角形的判定与性质解决简单的几何证明与计算问题;.会用相似三角形的判定与性质解决简单的几何证明与计算问题;22.通过对例题.通过对例题44、、55的求解,发展逻辑思维能力,领悟方程思想.的求解,发展逻辑思维能力,领悟方程思想.重点相似三角形的判定与性质的简单应用相似三角形的判定与性质的简单应用..难点合理选择相似三角形的判定与性质合理选择相似三角形的判定与性质教学准备学生活动形式讲练结合教学过程课题引入:课前练习一1.(1)两个相似三角形的相似比是1:16,则周长比是_____,面积比是_______;(2)两个相似三角形的周长比是1:9,则相似比是_____;(3)两个相似三角形的面积比是1:5,则相似比是_______.2.已知△ABC∽△A′B′C′,AB=9,A′B′=12.(1)若△ABC的周长是24,则△A′B′C′的周长为___;(2)若S△ABC=27,则S△A′B′C′=____.课前练习二3.已知△ABC∽△A′B′C′,AB=9,A′B′=12.(1)若两个三角形的周长之差为8,求这两个三角形的周长.(2)若两个三角形的面积之和为100,求这两个三角形的面积备注:知识呈现:新课探索一例题1已知:如图,在△ABC中,∠ACB=90゜,CD是边AB上的高.求证:(1)AC2=ADAB;(2)CD2=ADBD.证明:由CD是Rt△ABC斜边上的高,可得AC2=AD·AB①;BC2=BD·AB②;CD2=AD·BD.这一结论也是一条著名的定理,称之为“射影定理”.应用①②,两个结论也可证明勾股定理若在已知△ACD与△CBD相似的条件下,你能用三角形面积之间的关系来证明CD2=AD·BD吗?新课探索二例题2如图,已知点D、E分别在△ABC的边AB和AC上,DE∥BC,=,四边形DBCE的面积等于16.求△ABC的面积.解:课内练习一1.如图,△ABC中,∠ACB=90゜,CD是AB边上的高.(1)已知BD=4,CD=6,则AD=______;(2)已知BD=9,BC=15,则AB=______;(3)已知AB=13,CD=6,则AD=_____请说说第(3)小题你是怎么解的课内练习二2.如图,AB∥DC,AC∥DE,若S△ABC=9,S△DCE=4,则S△ACD=____.说说你是怎么想的?课内练习三3.(洞孔成像)如图,AB∥A′B′,根据图中尺寸,可知物象A′B′的长是物AB的长的.你能说出其中的道理吗?相似三角形的对应高的比等于相似比.课内练习四4.如图,梯形ABCD中,AD∥BC,∠ACD=∠B.课堂小结:相似三角形性质的应用*如图,CD是Rt△ABC斜边上的高.则AC2=ADAB,BC2=BDAB,CD2=ADBD.课外作业练习册,预习要求24.524.5相似三角形的性质(相似三角形的性质(44))课堂时间安排教师主导活动时间:20分学生主体活动时间:20分教学后记