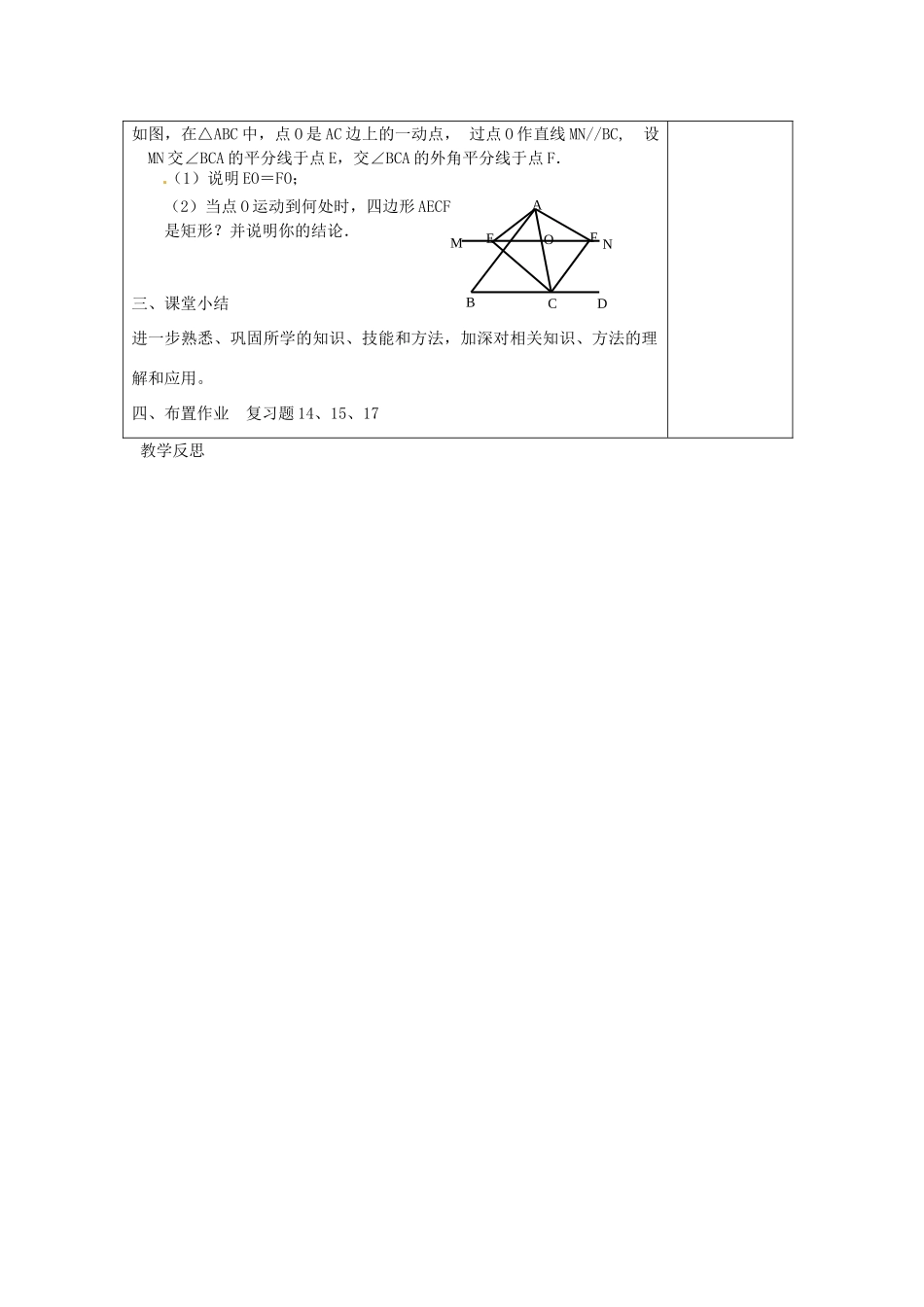
江苏省涟水县徐集中学八年级数学上册第三章中心对称图形(一)小结与思考教案苏科版教学过程教学活动内容个人主页一、例题教学例1:如图:△ABC和△ADE都是顶角为45°的等腰三角形,BC、DE分别是两个三角形的底边。图中的△ACE可以看成是哪个三角形通过怎样的旋转得到的?本题比较能体现旋转的内涵(旋转前后的图形全等;对应点到旋转中心的距离相等;每一对对应点与旋转中心的连线所成的角彼此相等)及等腰三角形的两腰相等的性质,使学生对旋转的性质及应用有更进一步的认识。例2:如图:ABCD的对角线相交于点O,过点O的直线分别与AD、BC相交于点E、F图中关于点O成中心对称的三角形、四边形有多少对?请将它们分别表示出来。FBDEADB梯行形CCBDEA通过本题教学,使学生进一步理解、掌握平行四边形的有关性质,掌握判定两个三角形或两个四边形成中心对称的方法,从而对中心对称图形有更进一步的认识。例3:如图:在菱形ABCD中,∠B=60°,点E、F分别在AB、AD上,且BE=AF。你能说明△ECF是等边三角形吗?(1)本题是通过有两边相等且有一个角是60°来说明三角形是等边三角形的,因为四边形ABCD是菱形,所以AB=BC=CD=DA,又因为∠B=60°,所以△ABC、△ACD都是等边三角形,所以BC=AC,∠B=∠CAD=60°,又因为BE=AF,所以根据“SAS”得:△CBE≌△CAF,从而得:CE=CF、∠BCE=∠ACF,又因为∠BCA=60°,所以∠ECF=60°,所以△ECF是等边三角形;(2)本题既复习了菱形、等边三角形和全等三角形的性质,又培养了学生探索能力及有条理的口头表述和书面表述能力。例4:如图:四边形ABCD的对角线相交于点O,且AD∥BC,AD=BC请补充2个条件,使四边形ABCD为正方形,并说明理由。[本题是开放题,解答多样;如:(1)AB=AD,AB⊥AD;(2)AB=AD,AC=BD;(3)AB⊥AD,AC⊥BD等,都可以说明四边形ABCD是正方形;所以通过本题教学,可以培养学生的发散思维能力,并且培养学生的口头表述能力和书面表述能力。二、解决问题ADBCFEABCOD如图,在△ABC中,点O是AC边上的一动点,过点O作直线MN//BC,设MN交∠BCA的平分线于点E,交∠BCA的外角平分线于点F.(1)说明EO=FO;(2)当点O运动到何处时,四边形AECF是矩形?并说明你的结论.三、课堂小结进一步熟悉、巩固所学的知识、技能和方法,加深对相关知识、方法的理解和应用。四、布置作业复习题14、15、17教学反思AEBCFONMD