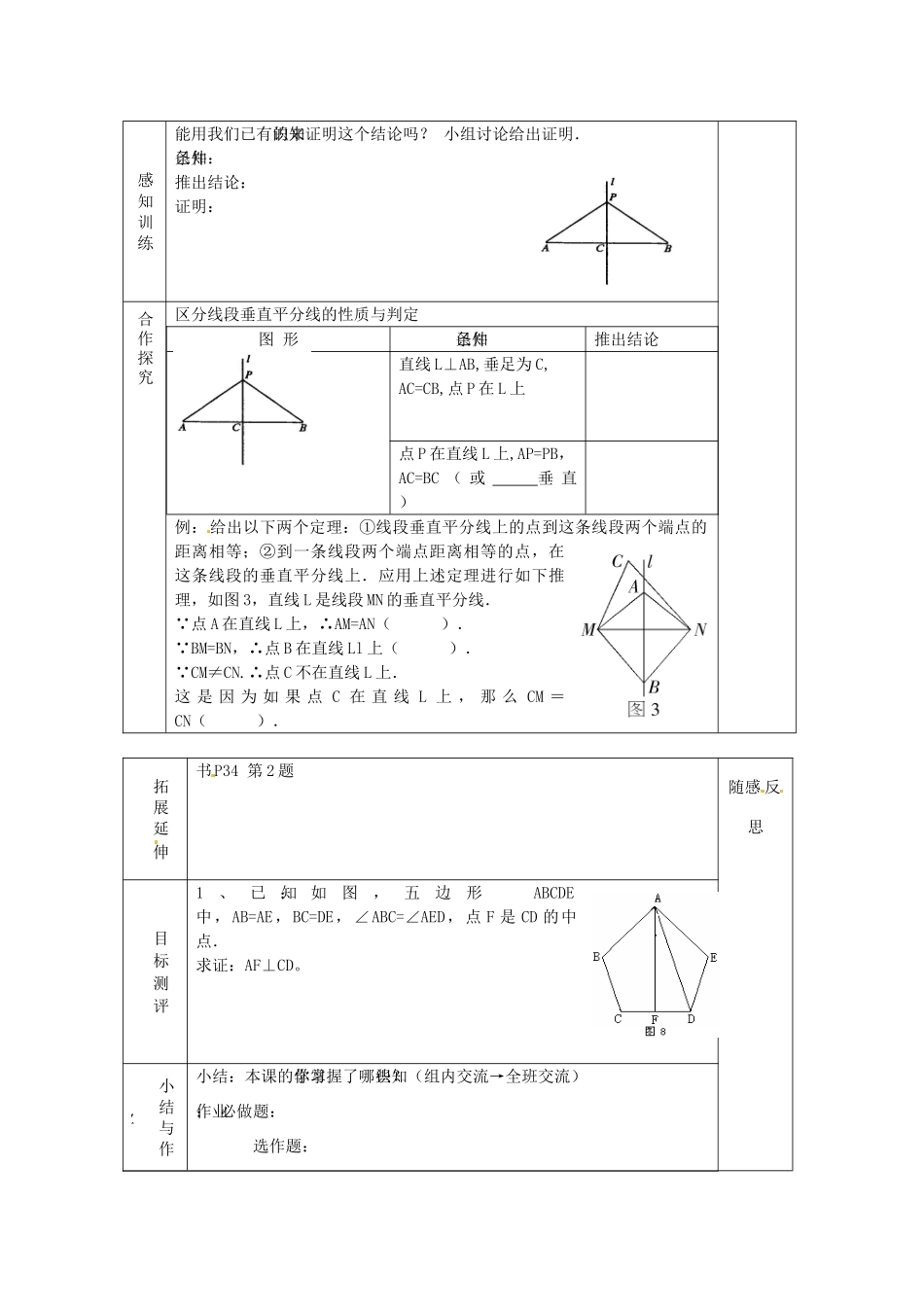
线段垂直平分线的性质年级八年级学科数学审核课题线段垂直平分线的性质学习目标1、探究线段垂直平分线的性质。2、能应用这两个性质解决一些简单的实际问题重点线段垂直平分线的性质及其应用。难点探索并总结出线段垂直平分线的性质,能运用其性质解答实际问题。预习导学[探究1]课本P33用平面图形将上述问题进行转化.作线段AB,取其中点P,过P作直线L,在直线L上取点P1、P2,连结AP1、AP2、BP1、BP2.会有以下两种可能、.图甲图乙讨论:要使L与AB垂直,AP1、AP2、BP1、BP2应满足什么条件?探究过程:1.如上图甲,若AP1≠BP1,那么沿L将图形折叠后,A与B,也就是∠APP1≠∠BPP1,即L与AB.2.如上图乙,若AP1=BP1,那么沿L将图形折叠后,A与B,就有∠APP1=∠BPP1,即L与AB.当AP2=BP2时,亦然.探究结论:与一条线段两个端点距离相等的点,在这条线段的垂直平分线上.也就是说在[探究1]中,只要使箭端到弓两端的端点的距离相等,就能保持射出箭的方向与木棒垂直.通过探究可以得到:与一条线段两个端点,在这条线段的。所以,线段的垂直平分线可以看成是。随感反思感知训练能用我们已有的知识来证明这个结论吗?小组讨论给出证明.已知条件:推出结论:证明:合作探究区分线段垂直平分线的性质与判定图形已知条件推出结论直线L⊥AB,垂足为C,AC=CB,点P在L上点P在直线L上,AP=PB,AC=BC(或垂直)例:给出以下两个定理:①线段垂直平分线上的点到这条线段两个端点的距离相等;②到一条线段两个端点距离相等的点,在这条线段的垂直平分线上.应用上述定理进行如下推理,如图3,直线L是线段MN的垂直平分线.∵点A在直线L上,∴AM=AN().∵BM=BN,∴点B在直线Ll上().∵CM≠CN.∴点C不在直线L上.这是因为如果点C在直线L上,那么CM=CN().拓展延伸书P34第2题随感反思目标测评1、已知:如图,五边形ABCDE中,AB=AE,BC=DE,∠ABC=∠AED,点F是CD的中点.求证:AF⊥CD。小结与作业小结:本课的学习你掌握了哪些知识?(组内交流→全班交流)作业:必做题:选作题: