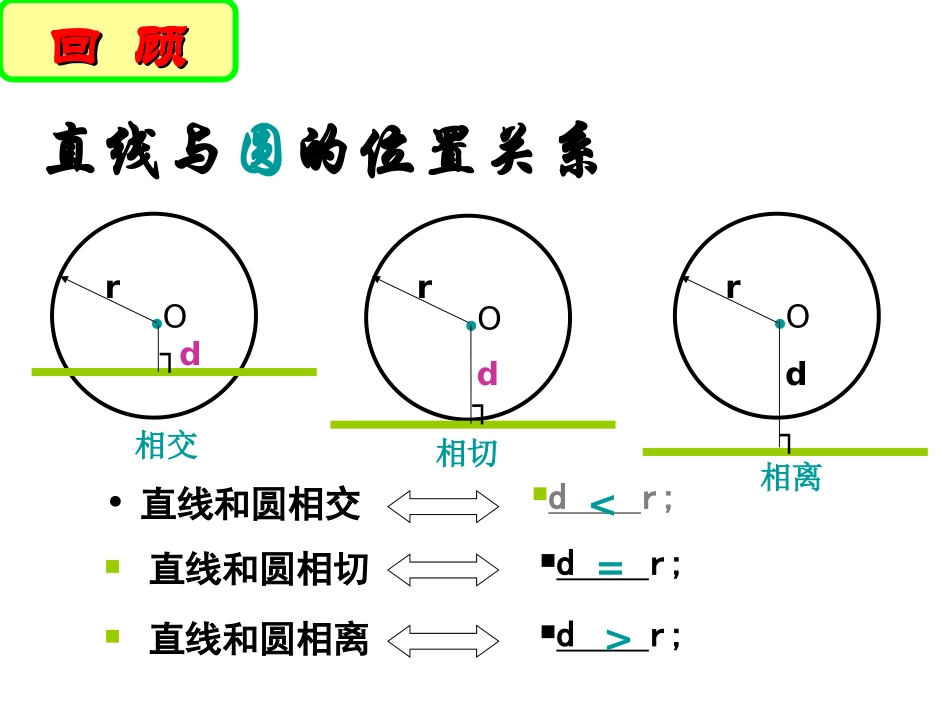
•直线和圆相交dr;dr;直线和圆相切直线和圆相离dr;直线与圆的位置关系●O●O相交●O相切相离rrr┐dd┐d┐<=>回顾回顾方法总结判定直线与圆的位置关系的方法有____种:(1)根据定义,由___________________________来判断;(2)根据性质,由___________________________的关系来判断。在实际应用中,常采用第二种方法判定。两直线与圆的公共点的个数圆心到直线的距离d与半径r1、已知圆的直径为13cm,设直线和圆心的距离为d:3)若d=8cm,则直线与圆______,直线与圆有____个公共点.2)若d=6.5cm,则直线与圆______,直线与圆有____个公共点.1)若d=4.5cm,则直线与圆,直线与圆有____个公共点.相交相切相离210小试身手3)若AB和⊙O相交,则.2、已知⊙O的半径为5cm,圆心O与直线AB的距离为d,根据条件填写d的范围:1)若AB和⊙O相离,则;2)若AB和⊙O相切,则;d>5cmd=5cmd<5cm小试身手直线与圆相切时,这条直线叫做圆的切线。5.5直线与圆的位置关系(二)——圆的切线的判定与性质rOA如图,OA是⊙O的半径,过A作直线⊥OA,若设圆的半径为r,直线与⊙O位置关系如何,为什么?ll探究探究因为圆心O到直线l的距离等于半径r,所以直线l与⊙O相切。rOA经过半径的外端并且垂直于这条半径的直线是圆的切线.切线的判定定理归纳归纳圆的切线判定判定一条直线是圆的切线有三种方法:1、利用定义:和圆只有一个公共点的直线是圆的切线。3、利用判定定理:经过半径的外端并且垂直于这条半径的直线是圆的切线。2、利用数量关系:到圆心的距离等于半径的直线是圆的切线。1、选择:下列直线能判定为圆的切线是()A、与圆有公共点的直线B、垂直于圆的半径的直线C、过圆的半径外端的直线D、到圆心的距离等于该圆半径的直线DD小试身手21DBOAC例1.△ABC内接于⊙O,AB是⊙O的直径,∠1=∠B,判断直线AD与⊙O的位置关系,并说明理由.典型例题典型例题当直线与圆有交点时,连接交点与圆心,证垂直.变一变:△ABC内接于⊙O,AB是⊙O的弦,∠1=∠B,判断直线AD与⊙O的位置关系,并说明理由.1DOACBE2当直线与圆有交点时,连接交点与圆心,证垂直.•如图,直线CD与⊙O相切于点A,直径AB与直线CD有怎样的位置关系?说说你的理由.CDB●OA探索交流探索交流E切线的性质定理圆的切线垂直于经过切点的半径.如图∵CD与⊙O相切于点A∴CD⊥OA.CD●OA已知直线和圆相切时:常连接切点与圆心。-----辅助线BAOPCPA、PB是⊙O的切线,切点分别为A、B,C是⊙O上一点,∠APB=40°,则∠ACB=。变一变:求弦AB所对的圆周角的度数。小试身手D例2、如图,AB为⊙O的直径,C为⊙O上一点,AD和过点C的切线互相垂直,垂足为点D。求证:AC平分∠DAB。看到切线,想到垂直。例3.点O是∠DPC的角平分线上的一点,⊙O与PD相切于A,求证:PC与⊙O相切.DCBAOPE典型例题典型例题当不明确直线与圆有无交点时,过圆心作直线的垂线,证明垂线段的长等于半径.OABCDE如图:AB为⊙O直径,⊙O过BC中点D,DE⊥AC,垂足为E.求证:DE是⊙O的切线。课堂反馈课堂反馈若已知直线过圆上一点,则连半径,证垂直;12(2011年.南京)如图,在Rt△ABC中,∠ACB=90°,AC=6㎝,BC=8㎝,P为BC的中点.动点Q从点P出发,沿射线PC方向以2㎝/s的速度运动,以P为圆心,PQ长为半径作圆.设点Q运动的时间为ts.⑴当t=1.2时,判断直线AB与⊙P的位置关系,并说明理由;⑵略拓展提升拓展提升分析:(1)判断直线AB与⊙P的位置关系,即要求圆心P到直线AB的距离与圆半径PQ的关系即可.PQ很易求出为2.4;求圆心P到直线AB的距离就应作辅助线:过点P作PD⊥AB,垂足为D,由△PBD∽△ABC求出,从而得出结论.解:⑴直线AB与⊙P相切.如图,过点P作PDAB,⊥垂足为D.在RtABC△中,∠ACB=90°,∵AC=6cm,BC=8cm,∴∵P为BC的中点,∴PB=4cm。∵∠PDB=∠ACB=90°,∠PBD=ABC∠.∴△PBDABC∽△。∴∴∴PD=2.4cm当t=1.2时,PQ=2t=2.4cm∴PD=PQ,即圆心P到直线AB的距离等于⊙P的半径。∴直线AB与⊙P相切。PDPBACABPD461022ABACBC10cm拓展提升拓展提升(1)若已知直线过圆上一点,则连半径,证垂直;(2)若不明确直线是否过圆上一点,则作垂直,证半径。经过半径的外端并且垂直于这条半径的直线是圆的切线.1.切线的判定定理2.切线的性质定理圆的切线垂直于过切点的半径.3.证明一条直线是圆的切线时总结总结