正余弦函数的图像VIP免费

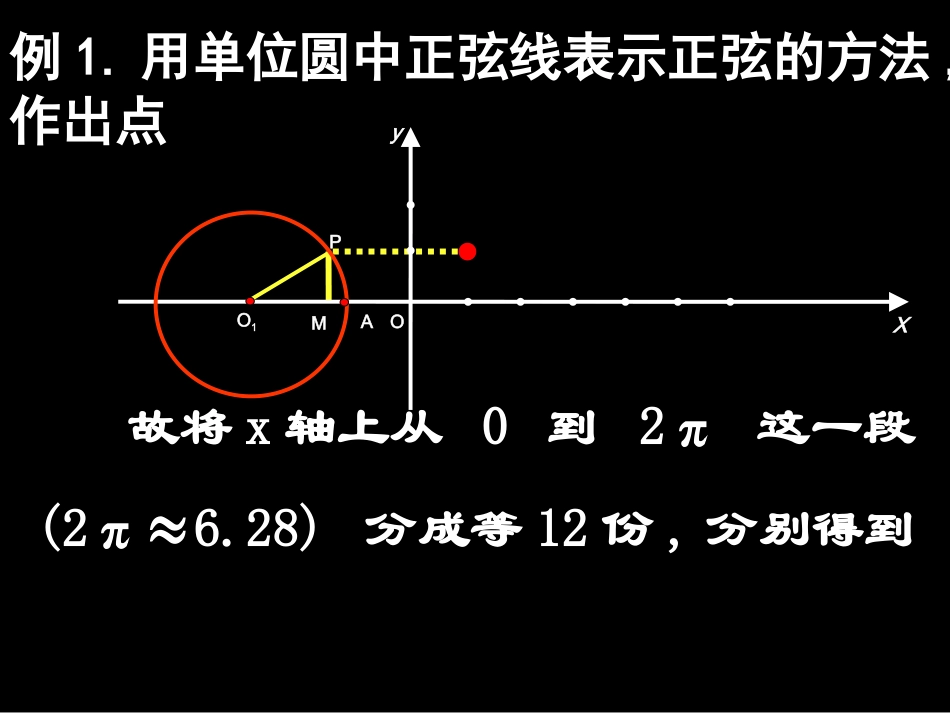
正弦函数、余弦函数的图像和性质（一）一.知识回顾1.三角函数是以角(实数)为自变量的函数.2.常用画图的方法:描点法y=sinx过点故介绍另一种画法几何法(即利用三角函数线画图)ysinx,xR,ycosx,xR(,sin),(,sin)66333sin0.866,32而不便于描点故将x轴上从0到2π这一段(2π≈6.28)分成等12份,分别得到例1.用单位圆中正弦线表示正弦的方法,作出点)6πsin6π(，PMO1OyXA)6πsin6π(，62π2,3π2,2π,3π,6π,0练习:用单位圆中正弦线表示正弦的方法作出点)3sin3(，MO1OyXA62P)3sin,3(仿上例可以作出y=sinx,x∈[0,2π]的图象xyo观察正弦曲线,得五个关键点即为正弦曲线与x轴的交点和曲线的最高点、最低点。在以后的画图过程中，经常先找出这五点，用光滑曲线将它们连接起来，就得到正弦函数的简图，这种作图的方法称“五点（画图）法”1-12322523232(0,0),(,1),2(,0),3(,1),2(2,0)yy=cosx故余弦函数的图象可通过将正弦曲线向左平移个单位长度而得到,余弦函数的图象叫余弦曲线.xo=sin(x+)1-1观察余弦曲线,得五个关键点即为余弦曲线与x轴的交点和曲线的最高点,最低点。223522322232(0,1),(,0),2(,1),3(,0),2(2,1)yY=sinxy=cosxxyoy=sinx,x[0∈，2π]练习：在同一直角坐标系中，用五点法作出下列图象⑴y=sinxx∈[0，2π]⑵y=cosxx∈y=cosx,x∈向右平移3[,]223[,]2223222y1-1前者y=sinx后者y=cosx=πsin(x+)2向左平移π个单位2后者y=cosxπ个单位2π前者y=sinx=cos(x-)2例2：画出函数的简图：y=1+sinx,x[0∈，2π]000012111-1y=1+sinx,x[0∈，2π]y=sinx,x[0∈，2π]y=sinx,x[0,2π]y=1+sinx,x[0,2π]∈∈解：按五个关键点列表：Xsinx1+sinx02πππ23π2π23π22π1个单位向上平移yxo211-10100-11-10yxO1y=-cosx,x[0,2π]∈y=cosx,x[0∈，2π]y=cosx,x[0∈，2π]与y=-cosx,x[0∈，2π]图象关于x轴对称解:找出y=-cosx,x[0∈，2π]五个关键点列表：Xcosx-cosx0π2π3π/2例3：画出函数的简图：y=-cosx,x∈[0，2π]π/221.利用单位圆中的正弦线画出正弦函数的图象——几何法优、缺点:画图准确但较繁琐。2.用五个关键点(与x轴的交点、曲线最高点及最低点）画图——五点法优、缺点：画图简捷但不够准确。知识小结:P64---1