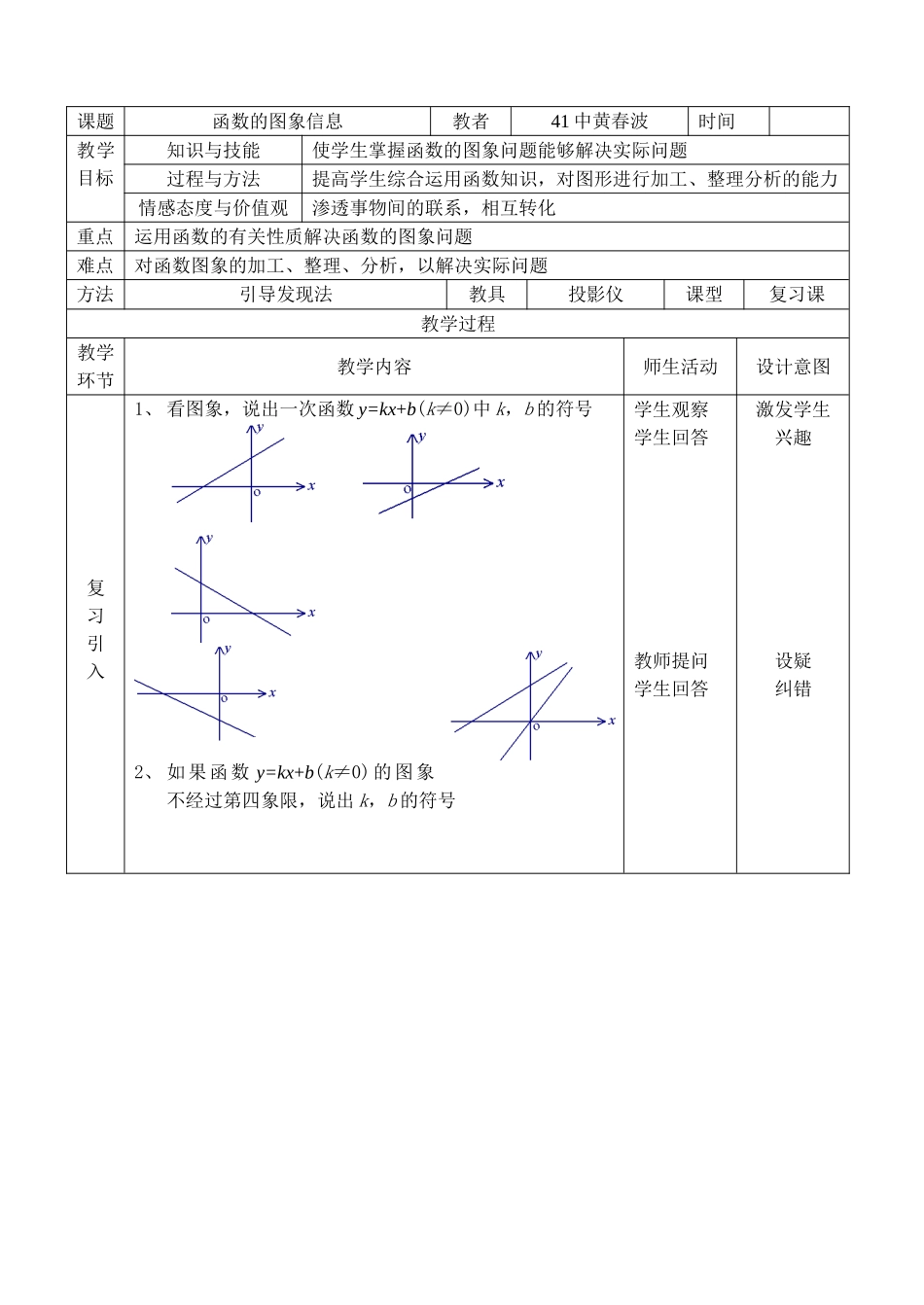
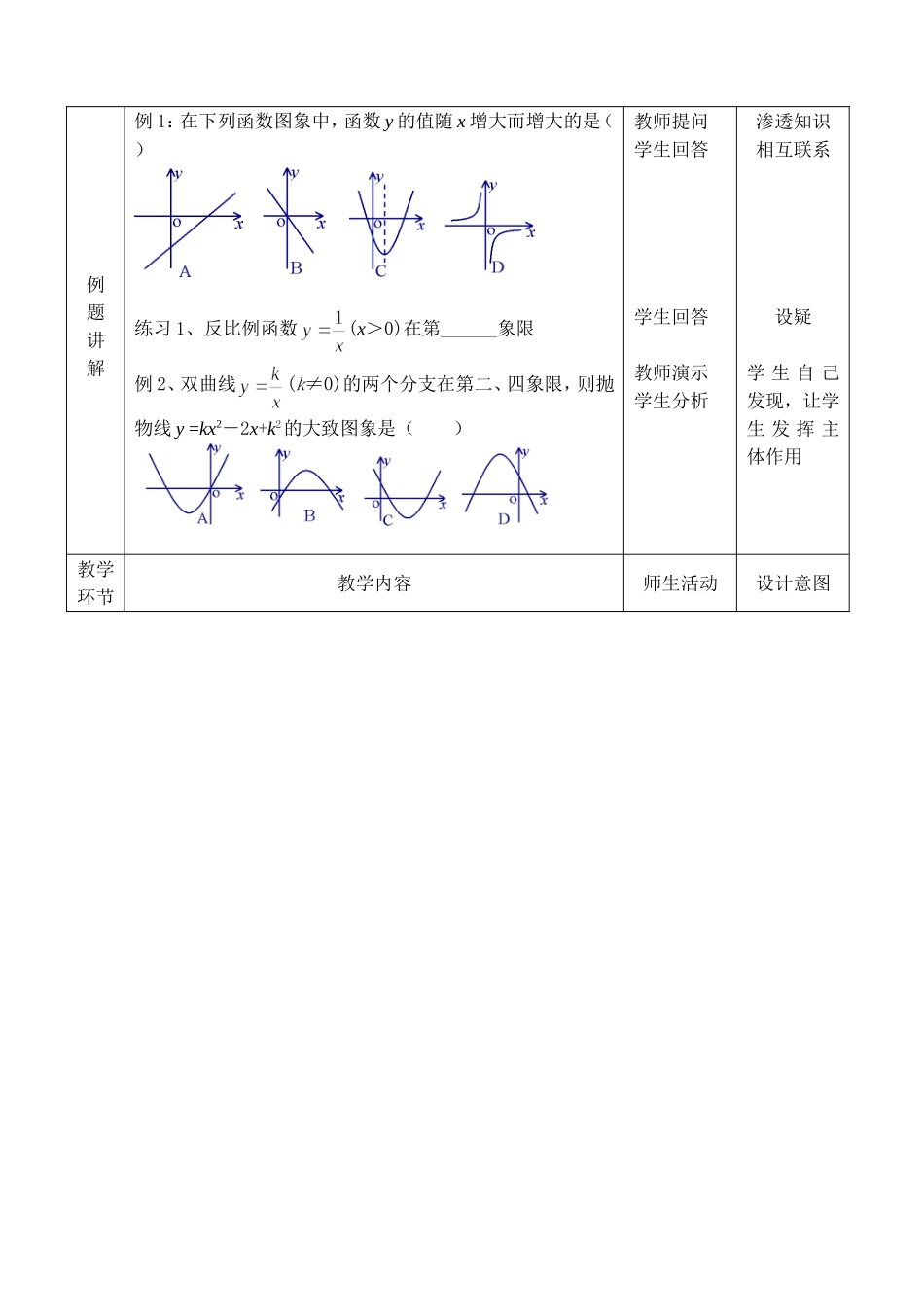
课题函数的图象信息教者41中黄春波时间教学目标知识与技能使学生掌握函数的图象问题能够解决实际问题过程与方法提高学生综合运用函数知识,对图形进行加工、整理分析的能力情感态度与价值观渗透事物间的联系,相互转化重点运用函数的有关性质解决函数的图象问题难点对函数图象的加工、整理、分析,以解决实际问题方法引导发现法教具投影仪课型复习课教学过程教学环节教学内容师生活动设计意图复习引入1、看图象,说出一次函数y=kx+b(k≠0)中k,b的符号2、如果函数y=kx+b(k≠0)的图象不经过第四象限,说出k,b的符号学生观察学生回答教师提问学生回答激发学生兴趣设疑纠错例题讲解例1:在下列函数图象中,函数y的值随x增大而增大的是()练习1、反比例函数(x>0)在第______象限例2、双曲线(k≠0)的两个分支在第二、四象限,则抛物线y=kx2-2x+k2的大致图象是()教师提问学生回答学生回答教师演示学生分析渗透知识相互联系设疑学生自己发现,让学生发挥主体作用教学环节教学内容师生活动设计意图教学讲解练习2、判断正误如图为二次函数y=ax2+bx+c图象的一部分,根据图象判断下列各题正误(1)a<0b>0c>0()(2)b2-4ac<0()(3)a+b+c<0()(4)a-b+c>0()练习3、二次函数y=ax2+bx+c图象如图,请你根据看到的图象信息,说出有关系数的符号。例3、已知函数y=ax2+bx+c图象如图所示,请你画出直线y=ax+b与双曲线在同一坐标系中大致图象例4、一定质量的二氧化碳,其体积v(m3)是密度ρ(kg/m3)的反比例函数,根据图中已知条件,写出ρ=1.1(kg/m3)时,二氧化碳体积v=________(m3)例5、假定甲、乙两人在一次赛跑中,路程s与时间t的关系如图所示,则可以知道1、这是一次_____m赛跑2、甲乙二人先到终点的是_________3、乙在这次赛跑中的速度________m/s练习4、汽车开始行驶时,油箱内有油40升,如果每小时耗油5升,则油箱内余油量Q(升)与行驶时间t(时)的函数关系图象表示应为()若汽车每小时行驶60千米,那么汽车最远能行驶多远就必须返回才能回到出发地?(设在途中不加油)教师引导学生发现动手画相关学科的应用学生分析观察回答教师指导学生分析猜想让学生主体作用充分发挥教学环节教学内容师生活动设计意图教学讲解练习5、如图有一个装有循环水系统的游泳池装有进出两种水管,设单位时间内进出水量是一定的,设从某时刻4小时内只进水不出水,在随后的8小时内为了过滤水启动循环系统,又进水又出水。得到水量y米3与时间x小时之间的函数关系1、求只进水不出水时y与x的函数关系式2、请说出M(10,700)的实际意义3、若12小时后只放水不进水,放完为止,求此时的y与x的函数关系式教师引导学生发现引导学生理论联系实际小结1、由图象给出数据信息对已获数据信息进行加工分清变量之间关系2、不忘检验,去伪存真,写出答案学生小结教师补充形成知识体系板书设计函数的图象信息一、判断符号型二、与相关学科的联系练习五例3三、在实际问题中应用