几何证明题（中档题）VIP免费

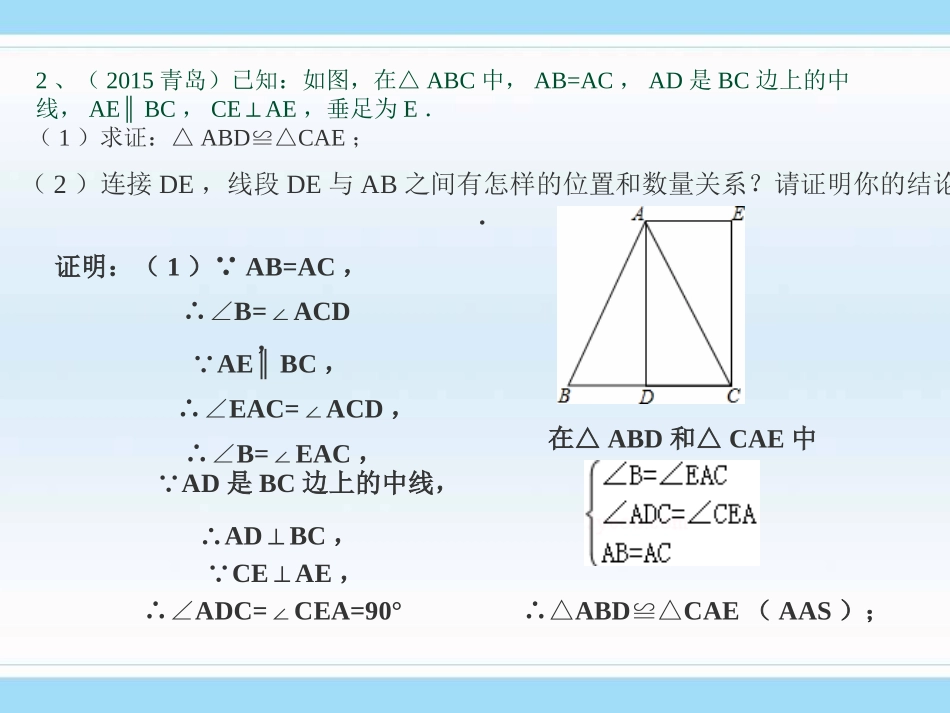
课前热身：1、（2014昆明）（本小题5分）已知：如图，点A、B、C、D在同一条直线上，AB=CD，AECF∥，且AE=CF.求证：∠E=F∠证明：∵AE∥CF，∴∠A=∠FCD，在△ABE和△CDF中，AB＝CD∠A＝∠FCDAE＝CF∴△ABE≌△CDF（SAS），∴∠E=∠F．2、（2015青岛）已知：如图，在△ABC中，AB=AC，AD是BC边上的中线，AE∥BC，CE⊥AE，垂足为E．（1）求证：△ABD≌△CAE；（2）连接DE，线段DE与AB之间有怎样的位置和数量关系？请证明你的结论．证明：（1）∵AB=AC，∴∠B=∠ACD，∵AE∥BC，∴∠EAC=∠ACD，∴∠B=∠EAC，∵AD是BC边上的中线，∴AD⊥BC，∵CE⊥AE，∴∠ADC=∠CEA=90°在△ABD和△CAE中∴△ABD≌△CAE（AAS）；2、（2015青岛）已知：如图，在△ABC中，AB=AC，AD是BC边上的中线，AE∥BC，CE⊥AE，垂足为E．（1）求证：△ABD≌△CAE；（2）连接DE，线段DE与AB之间有怎样的位置和数量关系？请证明你的结论．证明：（2）如右图：AB=DE，且AB∥DE，由（1）可得：△ABD≌△CAE∴BD=AE∵AE∥BC，即BD∥AE∴四边形ABDE是平行四边形，∴AB=DE，且AB∥DE，3、如图，已知在RtABC△中，∠C=900，AD是∠BAC的角分线.（1）以AB上的一点O为圆心，AD为弦在图中作出⊙O．（不写作法，保留作图痕迹）；（2）试判断直线BC与⊙O的位置关系，并证明你的结论；（1）解：如图为所求作的圆⊙O．（2）相切；证明：连结OD，∵OA=OD，∴∠OAD=ODA∠∵AD是∠BAC的平分线，则∠OAD=DAC∠，∴∠ODA=DAC∠，∴ODAC∥∴∠ODB=C=90°∠，∴ODBC⊥，即BC是⊙O的切线．5、如图，已知是⊙O的弦，半径OA＝2，OA和AB的长度是关于的一元二次方程的两个实数根．042axx（1）求弦的长度；（2）计算；AOBS（3）⊙O上一动点从点A出发，沿逆时针方向运动一周，当时，求点P所经过的弧长（不考虑点P与点B重合的情形）．AOBPOASSAOBP第5题图解：（1）由已知根据根与系数的关系：2+AB=4∴AB=2CP3P2P1AOBP（2）过点O作OCAB⊥于C，∵OCAB⊥∴AC=AB=1∠ACO=90°在RtACO△中2222213OCOAACOAB11=ABOC=23322S△CP3P2P1AOBP（3）如图，延长BO交⊙O于点，连结1AP∵点O是直径的中点1POA△AOB△∴S=S∠AOP＝120°∴的长度为1AP作点A关于直径的对称点，连结,．2P2AP2OP2POA△AOB△易得S=S∠AOP＝120°21∴的长度为2AP3834作点B关于半径OA的对称点，连结,．3P3AP3OP易得=SOAPS3AOB△0360AOP∴的长度为2AP32答：p点所经过的弧长分别为：、、。343832