函数的单调性课件VIP免费

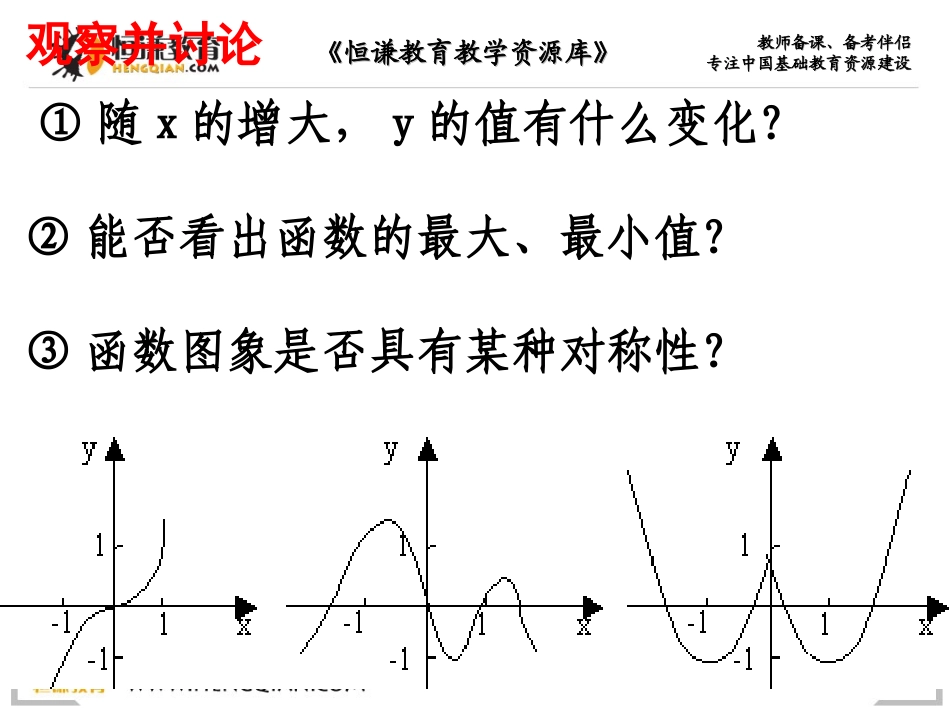
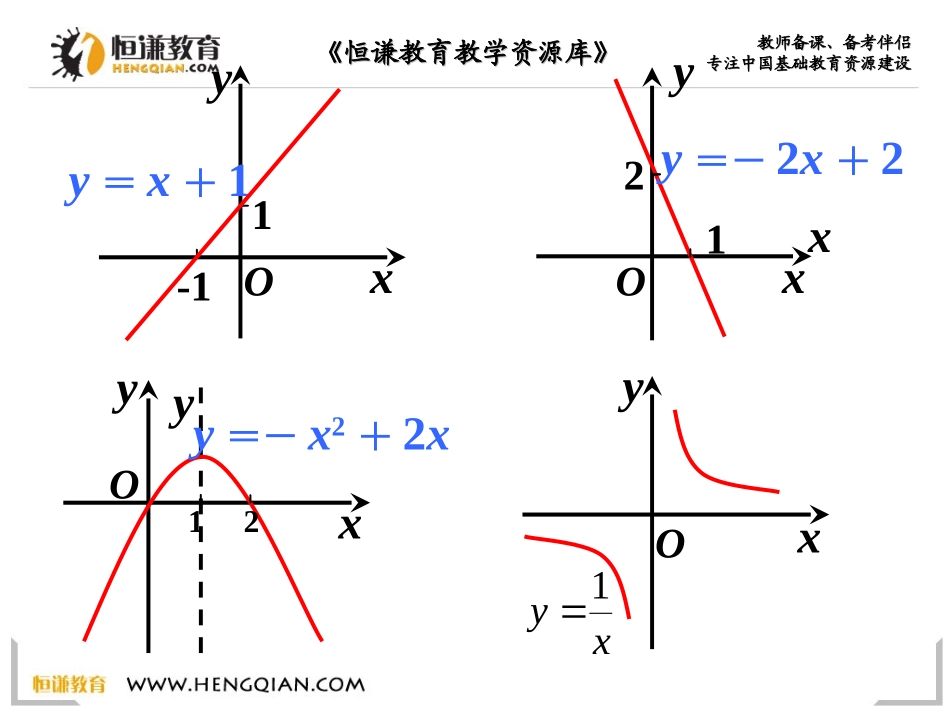
编辑发行：西安恒谦教育科技股份有限公司全国统一客服电话：编辑发行：西安恒谦教育科技股份有限公司全国统一客服电话：400-715-6688400-715-6688《恒谦教育教学资源库》《恒谦教育教学资源库》教师备课、备考伴侣教师备课、备考伴侣专注中国基础教育资源建设专注中国基础教育资源建设1.3函数的基本性质——单调性《恒谦教育教学资源库》《恒谦教育教学资源库》教师备课、备考伴侣教师备课、备考伴侣专注中国基础教育资源建设专注中国基础教育资源建设①随x的增大，y的值有什么变化？②能否看出函数的最大、最小值？③函数图象是否具有某种对称性？观察并讨论《恒谦教育教学资源库》《恒谦教育教学资源库》教师备课、备考伴侣教师备课、备考伴侣专注中国基础教育资源建设专注中国基础教育资源建设xy1x2yxOxy1y＝x＋11-1y21OOOyyxxy＝－2x＋2y＝－x2＋2x《恒谦教育教学资源库》《恒谦教育教学资源库》教师备课、备考伴侣教师备课、备考伴侣专注中国基础教育资源建设专注中国基础教育资源建设画出函数f(x)=x＋1、f(x)=-2x+2f(x)=x2的图像自左向右随x的增大，函数值怎样变化？xy＝x＋11-1Oyxy21Oy＝－2x＋2《恒谦教育教学资源库》《恒谦教育教学资源库》教师备课、备考伴侣教师备课、备考伴侣专注中国基础教育资源建设专注中国基础教育资源建设yx2xyO自左向右随x的增大，函数值怎样变化？《恒谦教育教学资源库》《恒谦教育教学资源库》教师备课、备考伴侣教师备课、备考伴侣专注中国基础教育资源建设专注中国基础教育资源建设如何用x与f(x)来描述上升的图象？Oxy学.科.网《恒谦教育教学资源库》《恒谦教育教学资源库》教师备课、备考伴侣教师备课、备考伴侣专注中国基础教育资源建设专注中国基础教育资源建设如何用x与f(x)来描述上升的图象？Oxy《恒谦教育教学资源库》《恒谦教育教学资源库》教师备课、备考伴侣教师备课、备考伴侣专注中国基础教育资源建设专注中国基础教育资源建设如何用x与f(x)来描述上升的图象？x2x1Oxyx1＜x2《恒谦教育教学资源库》《恒谦教育教学资源库》教师备课、备考伴侣教师备课、备考伴侣专注中国基础教育资源建设专注中国基础教育资源建设如何用x与f(x)来描述上升的图象？x2x1Oxyy＝f(x)f(x1)f(x2)x1＜x2f(x1)＜f(x2)在给定区间上任取x1,x2,若x1＜x2有f(x1)＜f(x2)函数f(x)在给定区间上为增函数.《恒谦教育教学资源库》《恒谦教育教学资源库》教师备课、备考伴侣教师备课、备考伴侣专注中国基础教育资源建设专注中国基础教育资源建设x1＜x2f(x1)＜f(x2)x2x1Oxyy＝f(x)f(x1)f(x2)在给定区间上任取x1,x2如何用x与f(x)来描述下降的图象？函数f(x)在给定区间上为增函数.yx2x1Oxy＝f(x)f(x1)f(x2)函数f(x)在给定区间上为减函数.x1＜x2f(x1)＞f(x2)在给定区间上任取x1,x2《恒谦教育教学资源库》《恒谦教育教学资源库》教师备课、备考伴侣教师备课、备考伴侣专注中国基础教育资源建设专注中国基础教育资源建设1.如果对于定义域I内的某个区间上的任意两个自变量的值x1,x2，当x1＜x2时，都有f(x1)＜f(x2)，那么就说f(x)在这个区间上是增函数.2.如果对于定义域I内的某个区间上的任意两个自变量的值x1,x2，当x1＜x2时，都有f(x1)＞f(x2)，那么就说f(x)在这个区间上是减函数.一般地，设函数f(x)的定义域为I.增函数、减函数的概念：《恒谦教育教学资源库》《恒谦教育教学资源库》教师备课、备考伴侣教师备课、备考伴侣专注中国基础教育资源建设专注中国基础教育资源建设如果函数y＝f(x)在某区间上是增函数或减函数，那么就说函数f(x)在这一区间具有(严格的)单调性，这一区间叫做y＝f(x)的单调区间.在单调区间上增函数的图象是上升的，减函数的图象是下降的.函数单调性的概念：《恒谦教育教学资源库》《恒谦教育教学资源库》教师备课、备考伴侣教师备课、备考伴侣专注中国基础教育资源建设专注中国基础教育资源建设-2321-1y-3-44Ox2-231-3-15-5函数y＝f(x)的单调区间有[－5,－2)，[－2,1)，[1,3)，[3,5]，其中y＝f(x)在[－5,－2)，[1,3)上是减函数，在区间[－2,1)，[3,5]上是增函数．图象法解：例1右图是定义在闭区间[－5,5]上的函数y＝f(x)的图象，根据图象说...