直线与椭圆的位置关系VIP免费

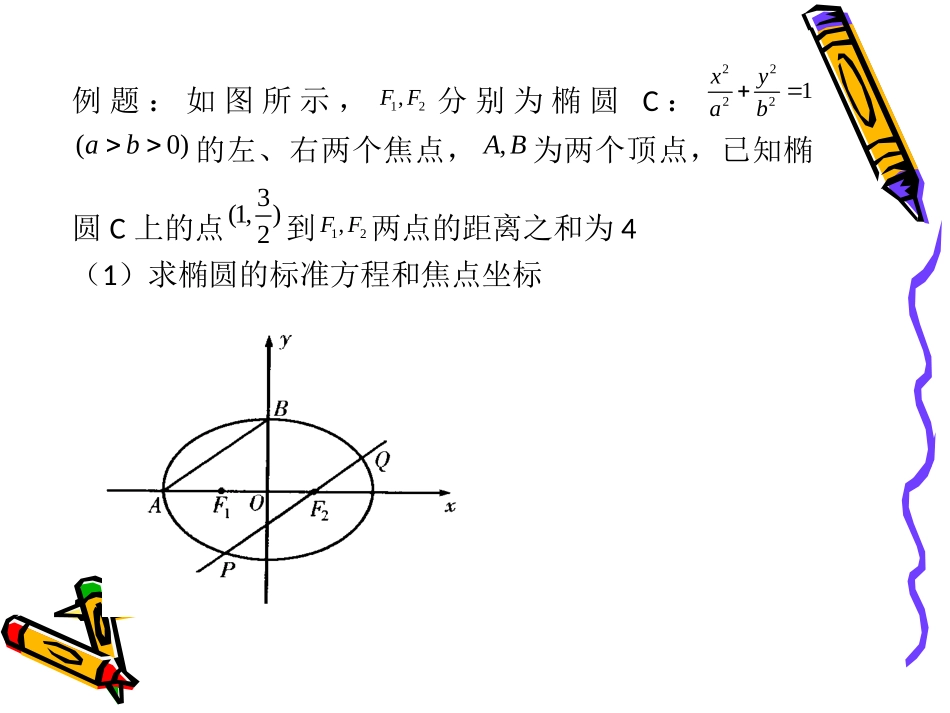
直线与椭圆的位置关系直线与椭圆的位置关系直线与椭圆的位置关系直线与椭圆的位置关系习题课习题课例题：如图所示，12,FF分别为椭圆C：22221xyab(0)ab的左、右两个焦点，,AB为两个顶点，已知椭圆C上的点3(1,)2到12,FF两点的距离之和为4（1）求椭圆的标准方程和焦点坐标（2）若直线与椭圆C有两个交点，求m的取值范围。变式1：直线与椭圆恒有公共点，求m的范围。变式1：直线与椭圆恒有公共点，求m的范围。22221(4)844014ykxmkxkxmxym分析：由消元得2222=(8k)-4(m+4k)(4-4m)6416160kmmm判别式k对任意的恒成立(3)若直线经过椭圆C的右焦点，且与椭圆C交与P，Q两点，求线段PQ的弦长。(4)若直线与椭圆C交与P，Q两点，且三角形OPQ的面积为627，其中O为坐标原点，求直线l的方程。变式2：若某直线l经过椭圆C的右焦点，与椭圆相交于M,N两点，求三角形OMN面积的最大值。变式2：若某直线l经过椭圆C的右焦点，与椭圆相交于M,N两点，求三角形OMN面积的最大值。11221,(,),(,)lxmyAxyBxy2分析：右焦点F（1,0），设直线为22221212221(43)69014369,4343xmymymyxymyyyymm由消元得小结：直线与椭圆位置关系的判断方法弦长公式求面积基本思想方法思考：若直线与椭圆C交与P，Q两点，是否存在m，使得以线段PQ为直径的圆经过坐标原点，若存在，求出m的值，若不存在，说明理由。