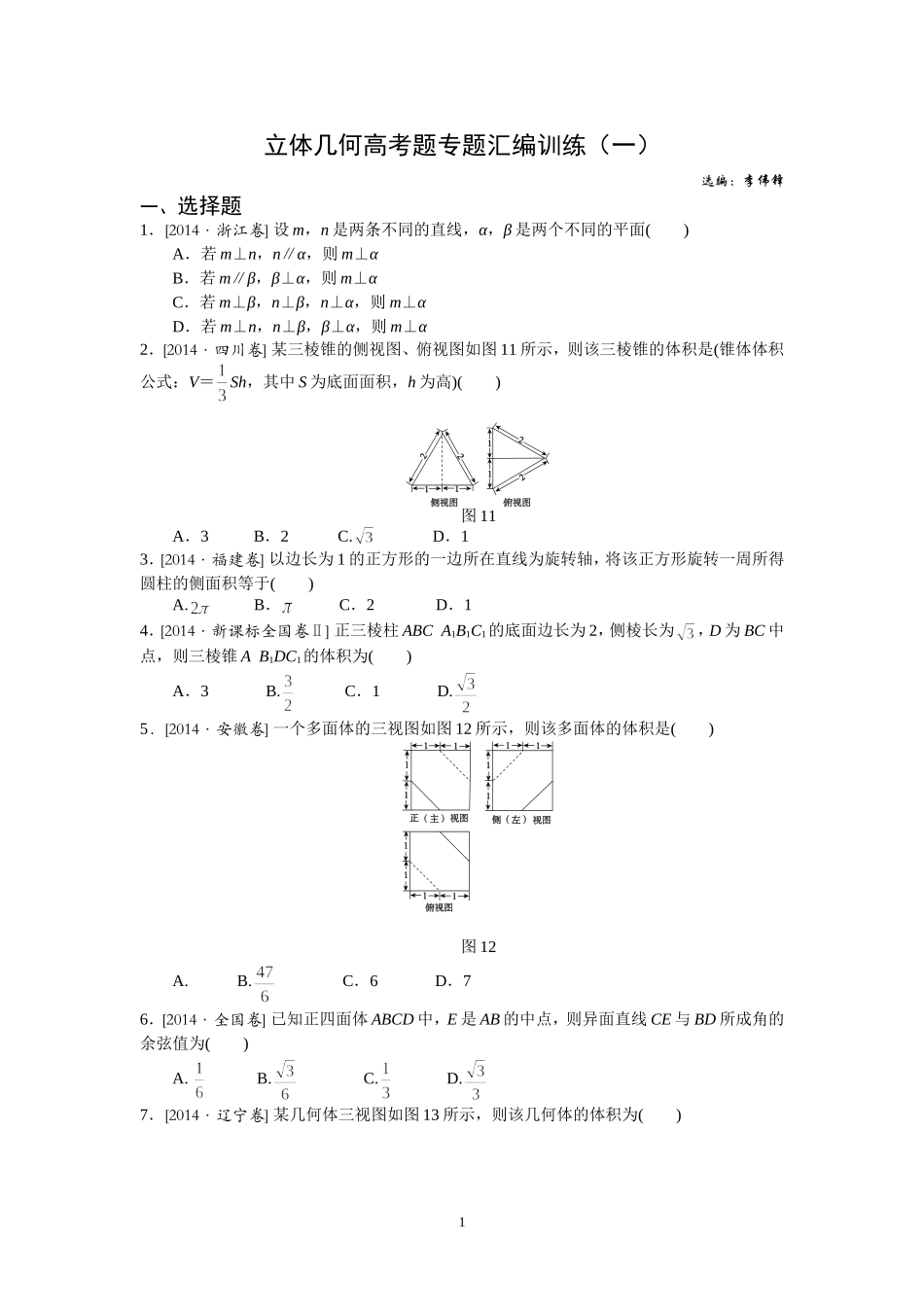
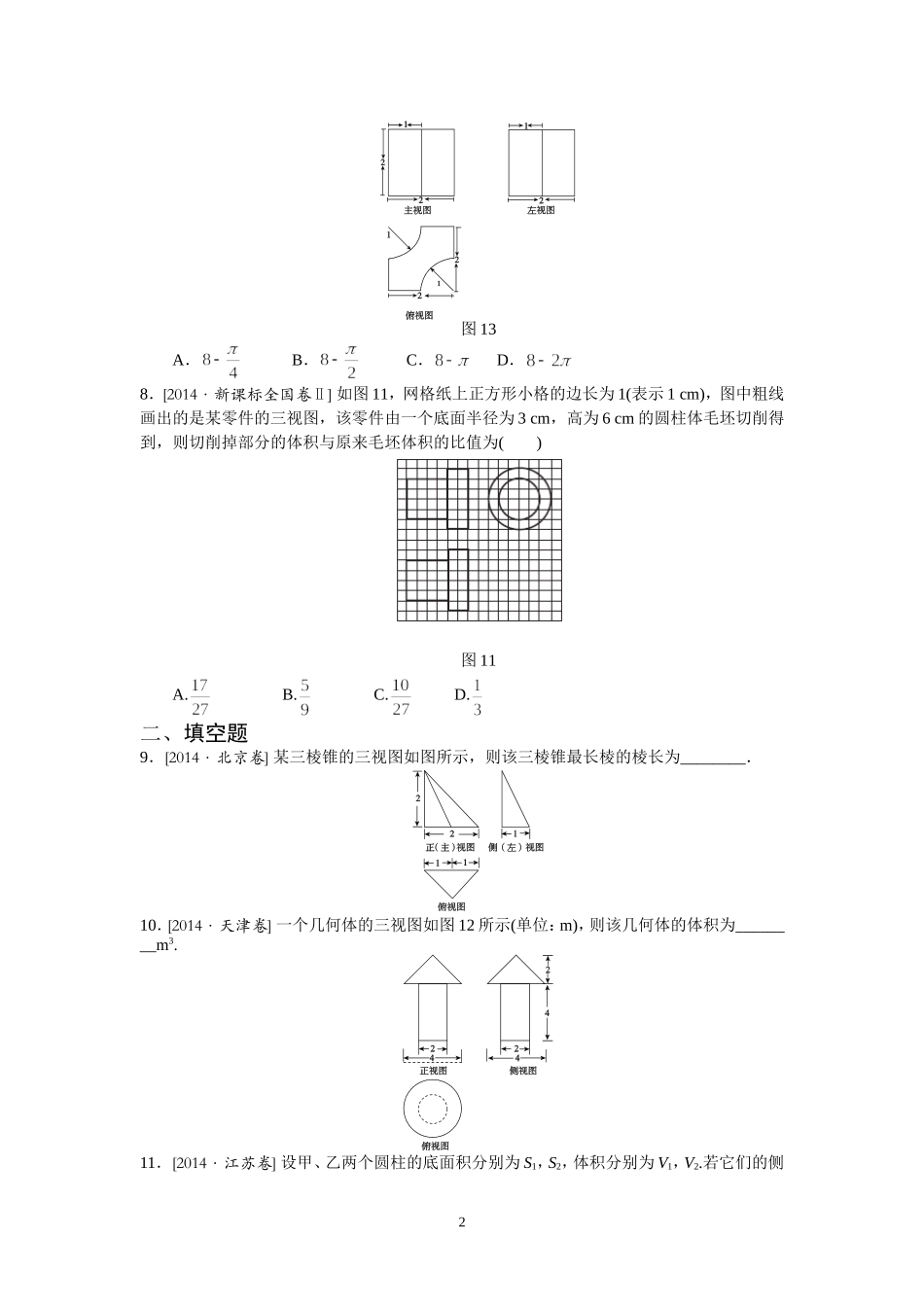
1立体几何高考题专题汇编训练(一)选编:李伟锋一、选择题1.[2014·浙江卷]设m,n是两条不同的直线,α,β是两个不同的平面()A.若m⊥n,n∥α,则m⊥αB.若m∥β,β⊥α,则m⊥αC.若m⊥β,n⊥β,n⊥α,则m⊥αD.若m⊥n,n⊥β,β⊥α,则m⊥α2.[2014·四川卷]某三棱锥的侧视图、俯视图如图11所示,则该三棱锥的体积是(锥体体积公式:V=Sh,其中S为底面面积,h为高)()图11A.3B.2C.D.13.[2014·福建卷]以边长为1的正方形的一边所在直线为旋转轴,将该正方形旋转一周所得圆柱的侧面积等于()A.B.C.2D.14.[2014·新课标全国卷Ⅱ]正三棱柱ABCA1B1C1的底面边长为2,侧棱长为,D为BC中点,则三棱锥AB1DC1的体积为()A.3B.C.1D.5.[2014·安徽卷]一个多面体的三视图如图12所示,则该多面体的体积是()图12A.B.C.6D.76.[2014·全国卷]已知正四面体ABCD中,E是AB的中点,则异面直线CE与BD所成角的余弦值为()A.B.C.D.7.[2014·辽宁卷]某几何体三视图如图13所示,则该几何体的体积为()2图13A.B.C.D.8.[2014·新课标全国卷Ⅱ]如图11,网格纸上正方形小格的边长为1(表示1cm),图中粗线画出的是某零件的三视图,该零件由一个底面半径为3cm,高为6cm的圆柱体毛坯切削得到,则切削掉部分的体积与原来毛坯体积的比值为()图11A.B.C.D.二、填空题9.[2014·北京卷]某三棱锥的三视图如图所示,则该三棱锥最长棱的棱长为________.10.[2014·天津卷]一个几何体的三视图如图12所示(单位:m),则该几何体的体积为________m3.11.[2014·江苏卷]设甲、乙两个圆柱的底面积分别为S1,S2,体积分别为V1,V2.若它们的侧3面积相等,且,则的值是________.12.[2014·山东卷]一个六棱锥的体积为,其底面是边长为2的正六边形,侧棱长都相等,则该六棱锥的侧面积为________.三、解答题:13.[2014·安徽卷]如图15所示,四棱锥PABCD的底面是边长为8的正方形,四条侧棱长均为.点G,E,F,H分别是棱PB,AB,CD,PC上共面的四点,平面GEFH⊥平面ABCD,BC∥平面GEFH.图15(1)证明:GH∥EF;(2)若EB=2,求四边形GEFH的面积.14.[2014·北京卷]如图15,在三棱柱ABCA1B1C1中,侧棱垂直于底面,AB⊥BC,AA1=AC=2,BC=1,E,F分别是A1C1,BC的中点.图15(1)求证:平面ABE⊥平面B1BCC1;(2)求证:C1F∥平面ABE;(3)求三棱锥EABC的体积.4立体几何专题汇编训练(一)答案解析:1.C[解析]A,B,D中m与平面α可能平行、相交或m在平面内α;对于C,若m⊥β,n⊥β,则m∥n,而n⊥α,所以m⊥α.故选C.2.D[解析]由图可知,三棱锥的底面为边长为2的正三角形,左侧面垂直于底面,且为边长为2的正三角形,所以该三棱锥的底面积S=×2×,高h=,所以其体积V=Sh=××=1,故选D.3.A[解析]由题意可知,该正方形旋转一周后所得的圆柱的底面半径r=1,高h=1,则该圆柱的侧面积S=2πrh=2π,故选A.4.C[解析]因为D为BC的中点,所以AD⊥BC,故AD⊥平面BCC1B1,且AD=,所以V三棱锥AB1DC1=S△B1DC1×AD=×B1C1×BB1×AD=××2××=1.5.A[解析]如图所示,由三视图可知该几何体是棱长为2的正方体截去两个小三棱锥后余下的部分,其体积V=8-2×××1×1×1=5.6.B[解析]如图所示,取AD的中点F,连接EF,CF,则EF∥BD,故EF与CE所成的角即为异面直线CE与BD所成的角.设正四面体的棱长为2,则CE=CF=,EF=1.在△CEF中,cos∠CEF===,所以异面直线CE与BD所成角的余弦值为.7.C[解析]根据三视图可知,该几何体是正方体切去两个体积相等的圆柱的四分之一后余下的部分,故该几何体体积V=23-×π×12×2=8-π.8.C[解析]该零件是一个由两个圆柱组成的组合体,其体积V=π×32×2+π×22×4=34π(cm3),原毛坯的体积V毛坯=π×32×6=54π(cm3),被切部分的体积V切=V毛坯-V=54π-34π=20π(cm3),所以==.9.2[解析]该三棱锥的直观图如图所示,并且PB⊥平面ABC,PB=2,AB=2,AC=BC=,PA==2,PC==,故PA最长.10.[解析]由三视图可知,该几何体为圆柱与圆锥的组合体,其体积V=π×12×4+π×22×2=.11.[解析]因为===,所以=.又圆柱的侧面积S侧=2πrh,所以S侧1=2π...