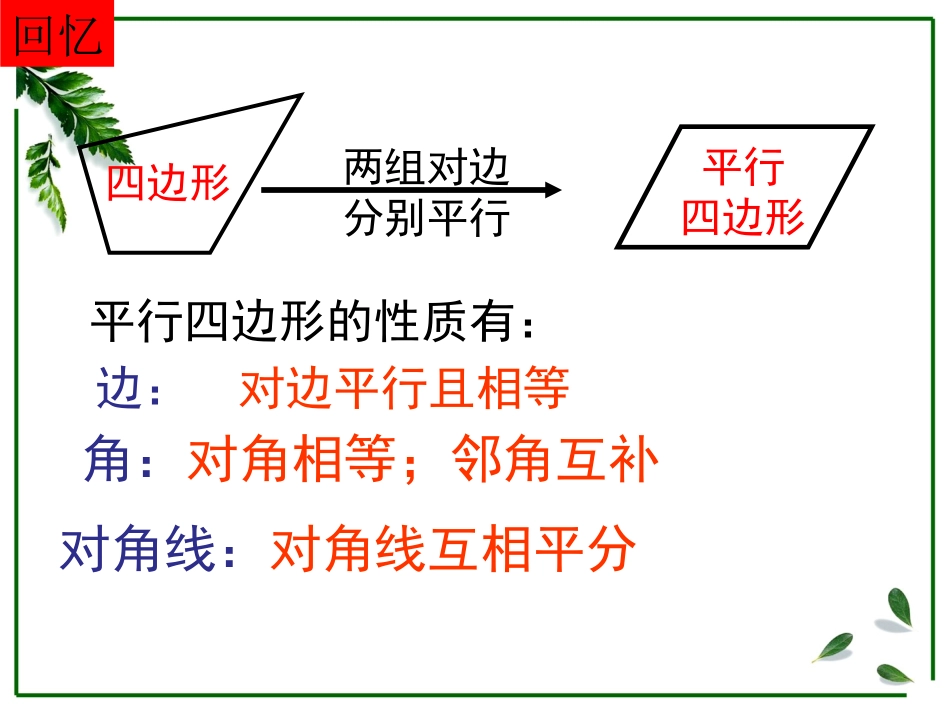
18.218.2特殊的平行四边形特殊的平行四边形118.2.18.2.1矩形矩形第第11课时课时知识回顾:1.平行四边形有哪些性质?两组对边分别平行平行四边形四边形平行四边形的性质有:边:对边平行且相等角:对角相等;邻角互补对角线:对角线互相平分回忆CBADCBADCBAD3.在推动平行四边形的过程中,什么发生变化了?什么没变?2.我们都知道三角形具有稳定性,平行四边形也具有稳定性吗?定义:有一个角是直角的平行四边形叫做矩形.四边形平行四边形矩形DCABABCD探究:矩形具有哪些性质?已知:如图,四边形ABCD是矩形求证:∠A=B=C=D=90°∠∠∠ABCD证明:∵四边形ABCD是矩形∴∠A=90°又矩形ABCD是平行四边形∴∠A=CB=D∠∠∠∠A+B=90°∠∴∠A=B=C=D=90°∠∠∠即矩形的四个角都是直角猜想1:矩形的四个角都是直角.性质1:矩形的四个角都是直角.已知:如图,矩形ABCD.ADBC∴AC=BD.∵四边形ABCD是矩形,证明:∴∠ABC=∠DCB,AB=CD.∴△ABC≌△DCB(SAS)在△ABC和△DCB中,AB=DC∠ABC=∠DCBBC=CB∵求证:AC=BD.猜想2:矩形的对角线相等.性质2:矩形的对角线相等.1.矩形具有平行四边形的所有性质.2.矩形特有的性质:①矩形的四个角都是直角;②矩形的对角线相等.3.矩形是轴对称图形.归纳:矩形具有哪些性质?ABCDO矩形的对角线把矩形分成四个等腰三角形,其中,相对的两个三角形全等.思考:矩形的两条对角线把矩形分成四个什么三角形?它们之间有什么关系?ABCDO◆四个全等的直角三角形.观察图中的Rt△ABC,在Rt△ABC中,BO是斜边AC上的中线,BO与AC有什么关系?ACBDBO2121根据矩形的性质,可以得到:直角三角形斜边上的中线等于斜边的一半.DCBA┓已知△ABC是Rt△,∠ABC=900,BD是斜边AC上的中线(1)若BD=3㎝则AC=㎝(2)若∠C=30°,AB=5㎝,则AC=㎝,BD=㎝.6510新知运用例:如图,矩形ABCD的两条对角线相交于点O,∠AOB=60°,AB=4㎝,求矩形对角线的长?方法小结:如果矩形两对角线的夹角是60°或120°,则其中必有等边三角形.∴∴ACAC与与BDBD相等且互相平相等且互相平分分∴∴OA=OBOA=OB∴△∴△AOBAOB是等边三角形是等边三角形∴∴OA=AB=4(OA=AB=4(㎝㎝))∴∴矩形的对角线长矩形的对角线长AC=BD=2OA=8AC=BD=2OA=8((㎝㎝))解:解:∵∵四边形四边形ABCDABCD是矩是矩形形DCBAo1.矩形具有而一般平行四边形不具有的性质是()A.对角线相等B.对边相等C.对角相等D.对角线互相平分2.下面性质中,矩形不一定具有的是()A.对角线相等B.四个角相等C.是轴对称图形D.对角线互相垂直AD练习:3、如图,在矩形ABCD中,AC与BD相交于点O,AB=3cm,BC=4cm则AC=cm,BO=cm,矩形的周长为cm,矩形的面积为cm2OADCB52.5练习:1412矩形的两条边和对角线构成一个三角形,是斜边.求矩形的边长和对角线的问题可转化为直角三角形,利用解决.直角对角线勾股定理快速回答1、已知矩形的两边长分别为8和6,则矩形的对角线长为.2、已知矩形的对角线长为3cm,一边长为2cm,则另一边长为.105cm•已知:四边形ABCD是矩形1.若已知AB=8㎝,AD=6㎝,则AC=_______㎝OB=_______㎝2.若已知∠DOC=120°,AC=8㎝,则AD=_____cmAB=_____cmODCBA510434课堂小结1.什么叫矩形?矩形有哪些性质?•有一个角是直角的平行四边形叫做矩形.•平行四边形矩形边角对角线对边平行且相等对角相等对角线互相平分对角线相等且互相平分四个角都是直角对边平行且相等课堂小结2.矩形的问题经常转化到等腰三角形或直角三角形中解决.补充:如图,把矩形纸片ABCD沿对角线AC折叠,点B落在点E处,EC与AD相交于点F.(1)求证:△FAC是等腰三角形;(2)若AB=4,BC=6,求△FAC的周长和面积.2.如图,在矩形ABCD中,AB=8,对角线BD比AD长4.求:①AD的长;②点A到BD的距离AE的长.作业:1.教材练习第1、2题.