圆周角 ()VIP免费

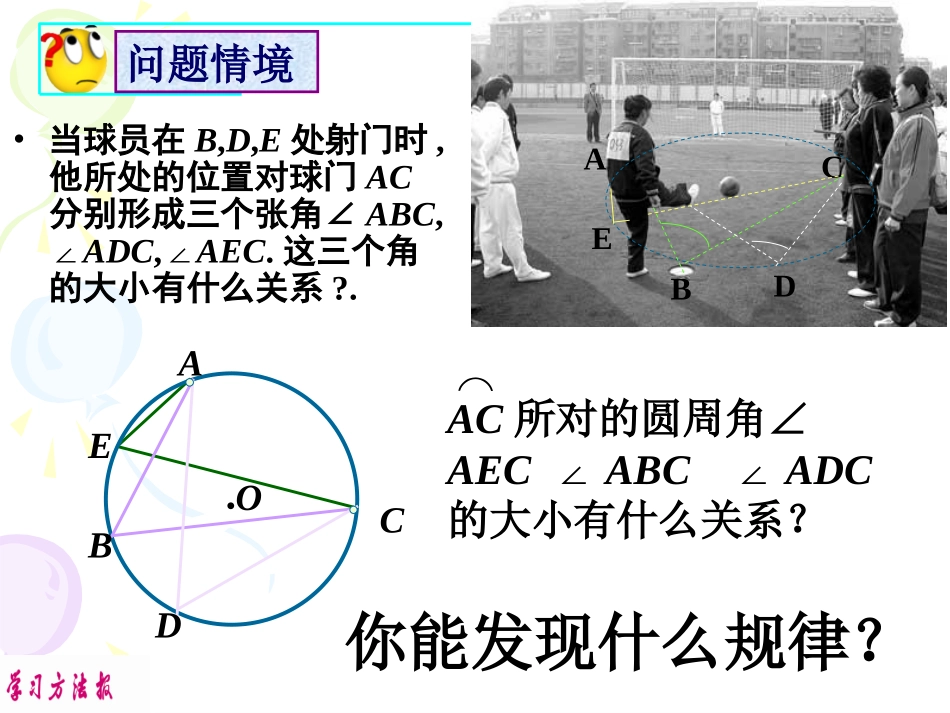
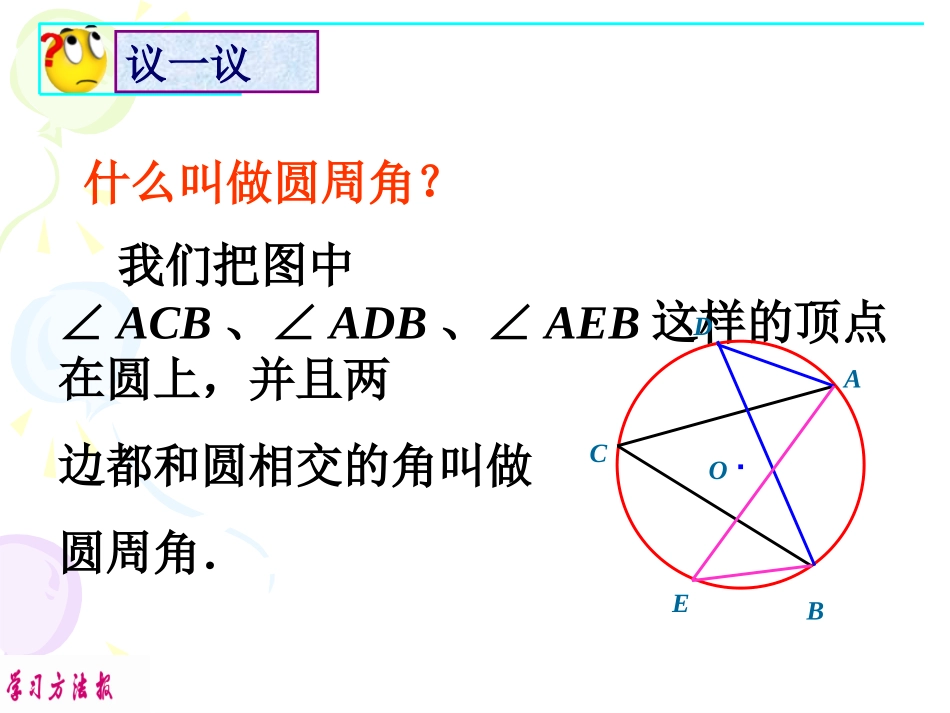
•当球员在B,D,E处射门时,他所处的位置对球门AC分别形成三个张角∠ABC,∠ADC,∠AEC.这三个角的大小有什么关系?.BACDEE●OBDCA你能发现什么规律？AC所对的圆周角∠AEC∠ABC∠ADC的大小有什么关系？⌒问题情境我们把图中∠ACB、∠ADB、∠AEB这样的顶点在圆上，并且两边都和圆相交的角叫做圆周角．什么叫做圆周角？·ABCDEO议一议下列圆中的是圆周角吗?抢抢答答√×√×√××××探究圆周角的性质：探究圆周角的性质：探究探究如图是一个圆柱形的海洋馆的横截面的示意图,人们可以通过其中的圆弧形玻璃AB观看窗内的海洋动物,同学甲站在圆心的O位置，同学乙站在正对着玻璃窗的靠墙的位置C，他们的视角（∠AOB和∠ACB）有什么关系？如果同学丙丁分别站在他靠墙的位置D和E，他们的视角（∠ADB和∠AEB）和同学乙的视角相同吗？·AB甲（O）乙（C）丙（D）丁（E）玻璃观察与思考·DABO可以发现，同弧所对的圆周角的度数没有变化，并且它的度数恰好等于这条弧所对的圆心角的度数的一半．C分别量一下图中所对的两个圆周角的度数，比较一下，再变动点C在圆周上的位置，圆周角的度数有没有变化？你能发现什么规律吗？再分别量出图中所对的圆周角和圆心角的度数，比较一下，你什么发现？ABAB观察与思考为了进一步探究上面的发现，如图在⊙O任取一个圆周角∠BAC，将圆对折，使折痕经过圆心O和∠BAC的顶点A．由于点A的位置的取法可能不同，这时折痕可能会；（1）在圆周角的一条边上；·COABBOCA21即 OA=OC，∴∠A=∠C．又∠BOC=∠A+∠C∴∠BOC=2∠A观察与思考（2）在圆周角的内部．圆心O在∠BAC的内部，作直径AD，利用（１）的结果，有12BADBOD12DACDOC1()2BADDACBODDOC12BACBOC·COABD观察与思考（3）在圆周角的外部．12BADBOD12DACDOC1()2DACDABDOCDOB12BACBOC圆心O在∠BAC的外部，作直径AD，利用（１）的结果，有·COABD观察与思考OFBACEG如图,圆中∠C=G∠,那么和的大小有什么关系?为什么?EF⌒⌒AB由此你又能得出什么结论?证明：连接OA、OB、OC、OD ∠C=∠AOB∠G=∠EOF∠C=∠G∴∠AOB=∠EOF∴AB=EF⌒⌒1212新知探究·ABC1OC2C3在同圆或等圆中，同弧或等弧所对的圆周角相等，都等于这条弧所对的圆心角的一半．定理半圆（或直径）所对的圆周角是直角，90°的圆周角所对的弦是直径．推论引入新知在同圆或等于圆中，如果两个圆周角相等它们所对弧一定相等吗？为什么？在同圆或等于圆中，如果两个圆周角相等，它们所对弧一定相等．因为，在同圆或等圆中，如果圆周角相等，那么它所对的圆心角也相等，因此它所对的弧也相等．练一练练一练1、如图，在⊙O中，∠ABC=50°，则∠AOC等于（）A、50°；B、80°；C、90°；D、100°ACBOD2、如图，△ABC是等边三角形，动点P在圆周的劣弧AB上，且不与A、B重合，则∠BPC等于（）A、30°；B、60°；C、90°；D、45°CABPB练一练练一练3、如图，∠A=50°，∠ABC=60°BD是⊙O的直径，则∠AEB等于（）A、70°；B、110°；C、90°；D、120°B4、如图，△ABC的顶点A、B、C都在⊙O上，∠C＝30°，AB＝2，则⊙O的半径是。ACBODECABO解：连接OA、OB ∠C=30°，∴∠AOB=60°又 OA=OB，∴△AOB是等边三角形∴OA=OB=AB=2，即半径为2。23.在⊙O中，一条弧所对的圆心角和圆周角分别为(2x+100)°和(5x-30)°，则x=__；2.如图，在直径为AB的半圆中，O为圆心，C、D为半圆上的两点，∠COD=50°，则∠CAD=______；20°25°拓展练习1.如图，点A、B、C、D在同一个圆上，四边形ABCD的对角线把4个内角分成8个角，这些角中哪些是相等的角？ABCD12345678∠1=4∠∠5=8∠∠2=7∠∠3=6∠课内练习例2如图，⊙O直径AB为10cm，弦AC为6cm，∠ACB的平分线交⊙O于D，求BC、AD、BD的长．86102222ACABBC·ABCDO解： AB是直径，∴∠ACB=∠ADB=90°．在Rt△ABC中，106））8例题解析又在Rt△ABD中，AD2+BD2=AB2，221052(cm)22ADBDAB CD平分∠ACB，∴AD=BD..ADBD例题解析例3求证：如果三角形一边上的中线等于这边的一半，那么这个三角形是直角三角形．（提示：作出以这条边为直径...