二面角的定义及求法举例VIP免费

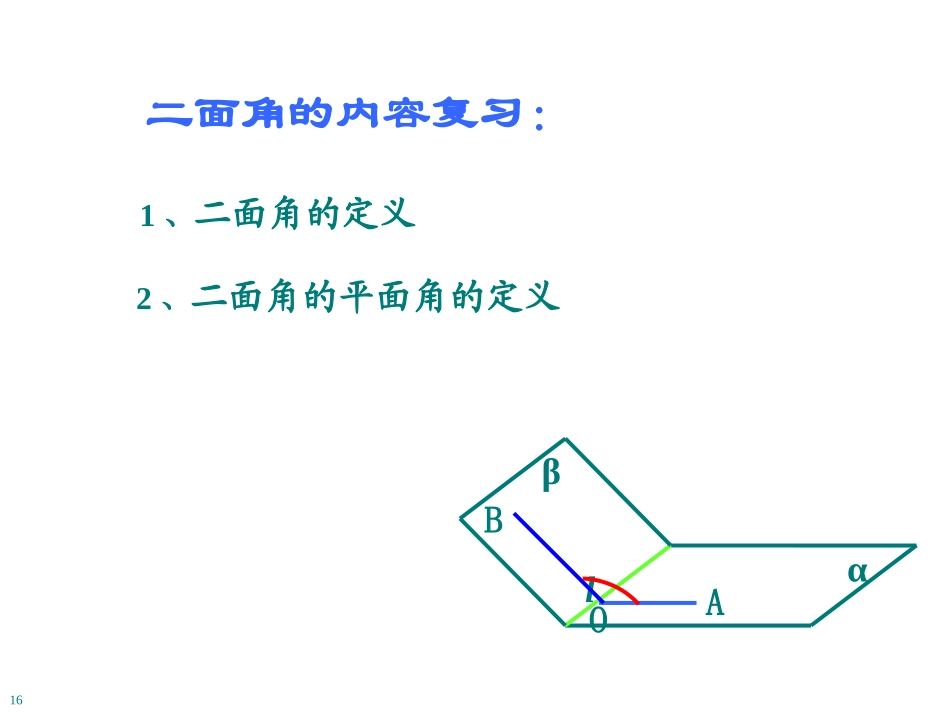
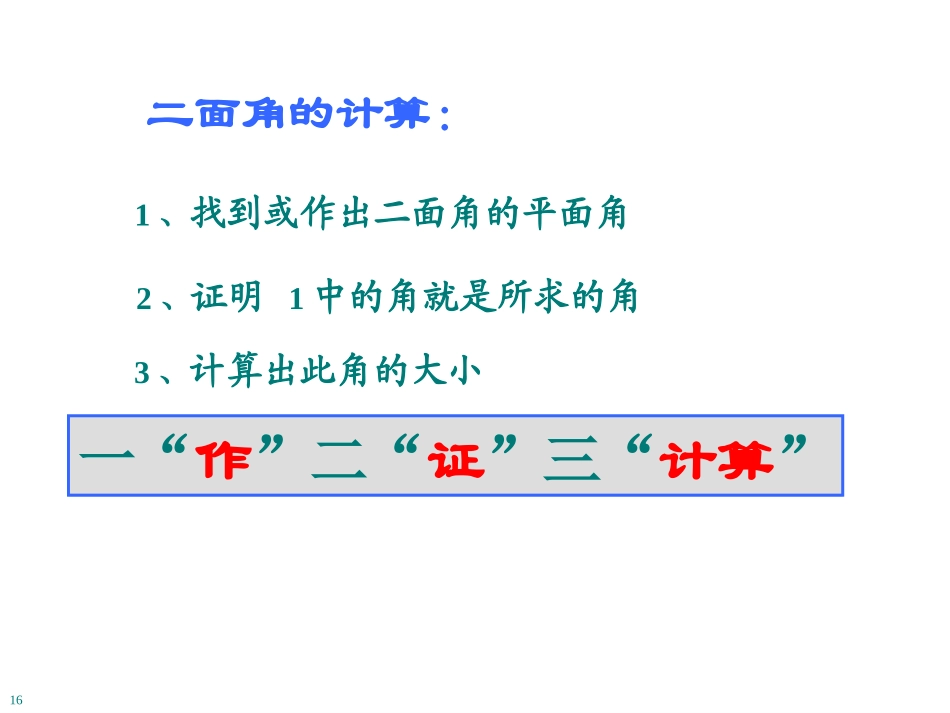
αβι二面角的内容复习：1、二面角的定义2、二面角的平面角的定义16lαβOAB二面角的计算：1、找到或作出二面角的平面角2、证明1中的角就是所求的角3、计算出此角的大小一“作”二“证”三“计算”16例1、已知正三棱锥V-ABC所有的棱长均相等，求二面角A-VC-B的余弦值的大小。VABC定义法BDCAS练习：如图，正四棱锥S-ABCD中，SA=SB=SC=SD=4,AB=BC=CD=DA=2,求侧面与底面所成二面角的余弦值大小？例2：三棱锥D-ABC中，DC=2a，DC⊥平面ABC，∠ACB=90o，AC=a，BC=2a，求二面角D-AB-C的正切值的大小。ＢＣＡＤ三垂线法5练习1：M、N分别是正方体ABCD-A1B1C1D1的棱AB、BC上的中点，求二面角N-B1M-B的余弦值的大小。ABCDA1B1C1D1MN32解：ABPlO例3．如图P为二面角内一点，PA⊥,PB⊥,且PA=5，PB=8，AB=7，求这二面角的度数。l设过PA、PB的平面PAB与棱l交于O点∵PA⊥∴PA⊥l∵PB⊥∴PB⊥l∴l⊥平面PAB∴∠AOB为二面角的平面角l又∵PA=5，PB=8，AB=7BPAPABBPAPP2cos222由余弦定理得∴∠P=60º∴∠AOB=120º∴所求二面角的度数为120º21垂面法变式：如图，四棱锥S-ABCD的底面是边长为1的正方形，SD⊥平面ABCD，SB=，求面SBC与面SAD所成求二面角的大小。345练习：正三棱柱ABC-A1B1C1中，AC=CC1，E∈B1B，平面AEC1⊥平面A1ACC1，求平面AEC1与平面ABC所成的二面角（锐角）的度数。B1BEC1ACEA1E45作二面角的平面角的常用方法①、点P在棱上②、点P在一个半平面上③、点P在二面角内lPABABPlABOlP—定义法—三垂线(逆)定理法—垂面法二面角如图，在四棱锥P—ABCD中，PA⊥底面ABCD，AB⊥AD，AC⊥CD，∠ABC＝60°，PA＝AB＝BC，E是PC的中点．(1)求PB和平面PAD所成的角的大小；(2)证明：AE⊥平面PCD；(3)求二面角A—PD—C的正弦值．课后练习如图，在四棱锥P—ABCD中，PA⊥底面ABCD，AB⊥AD，AC⊥CD，∠ABC＝60°，PA＝AB＝BC，E是PC的中点．(1)求PB和平面PAD所成的角的大小；(2)证明：AE⊥平面PCD；(3)求二面角A—PD—C的正弦值．(1)解在四棱锥P—ABCD中，因为PA⊥底面ABCD，AB⊂平面ABCD，故PA⊥AB.又AB⊥AD,PA∩AD＝A，从而AB⊥平面PAD，故PB在平面PAD内的射影为PA，从而∠APB为PB和平面PAD所成的角．在Rt△PAB中，AB＝PA，故∠APB＝45°.所以PB和平面PAD所成的角的大小为45°.如图，在四棱锥P—ABCD中，PA⊥底面ABCD，AB⊥AD，AC⊥CD，∠ABC＝60°，PA＝AB＝BC，E是PC的中点．(1)求PB和平面PAD所成的角的大小；(2)证明：AE⊥平面PCD；(3)求二面角A—PD—C的正弦值．(2)证明在四棱锥P—ABCD中，因为PA⊥底面ABCD，CD⊂平面ABCD，故CD⊥PA.由条件CD⊥AC，PA∩AC＝A，∴CD⊥平面PAC.又AE⊂平面PAC，∴AE⊥CD.由PA＝AB＝BC，∠ABC＝60°，可得AC＝PA.∵E是PC的中点，∴AE⊥PC.又PC∩CD＝C，综上得AE⊥平面PCD.如图，在四棱锥P—ABCD中，PA⊥底面ABCD，AB⊥AD，AC⊥CD，∠ABC＝60°，PA＝AB＝BC，E是PC的中点．(1)求PB和平面PAD所成的角的大小；(2)证明：AE⊥平面PCD；(3)求二面角A—PD—C的正弦值．(3)解过点E作EM⊥PD，垂足为M，连接AM，如图所示．由(2)知，AE⊥平面PCD，AM在平面PCD内的射影是EM，则可证得AM⊥PD.因此∠AME是二面角A—PD—C的平面角．由已知，可得∠CAD＝30°.设AC＝a，可得如图，在四棱锥P—ABCD中，PA⊥底面ABCD，AB⊥AD，AC⊥CD，∠ABC＝60°，PA＝AB＝BC，E是PC的中点．(1)求PB和平面PAD所成的角的大小；(2)证明：AE⊥平面PCD；(3)求二面角A—PD—C的正弦值．PA＝a，AD＝233a，PD＝213a，AE＝22a.在Rt△ADP中，∵AM⊥PD，∴AM·PD＝PA·AD，则AM＝PA·ADPD＝a·233a213a＝277a.如图，在四棱锥P—ABCD中，PA⊥底面ABCD，AB⊥AD，AC⊥CD，∠ABC＝60°，PA＝AB＝BC，E是PC的中点．(1)求PB和平面PAD所成的角的大小；(2)证明：AE⊥平面PCD；(3)求二面角A—PD—C的正弦值．在Rt△AEM中，sin∠AME＝AEAM＝144.所以二面角A—PD—C的正弦值为144.