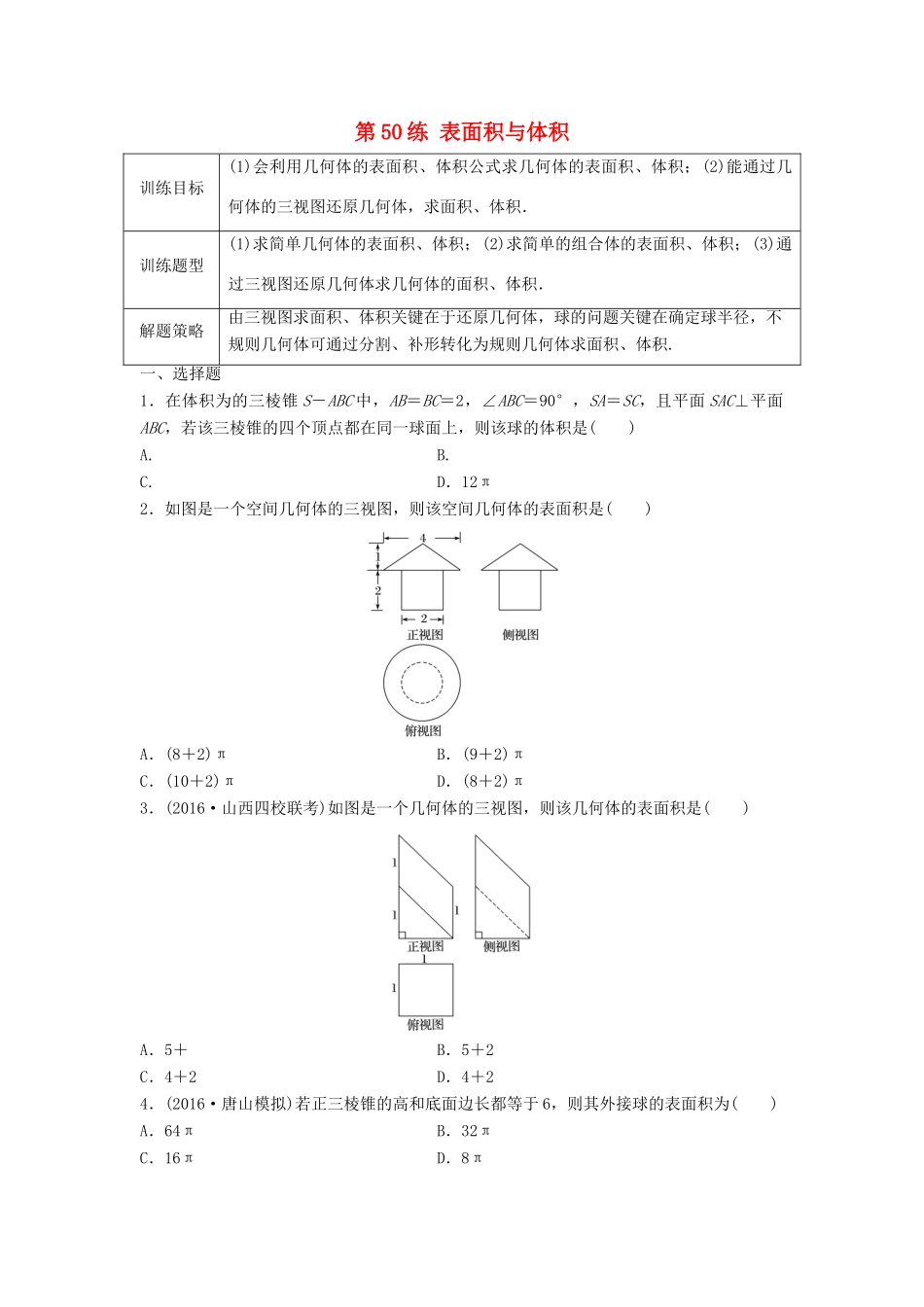
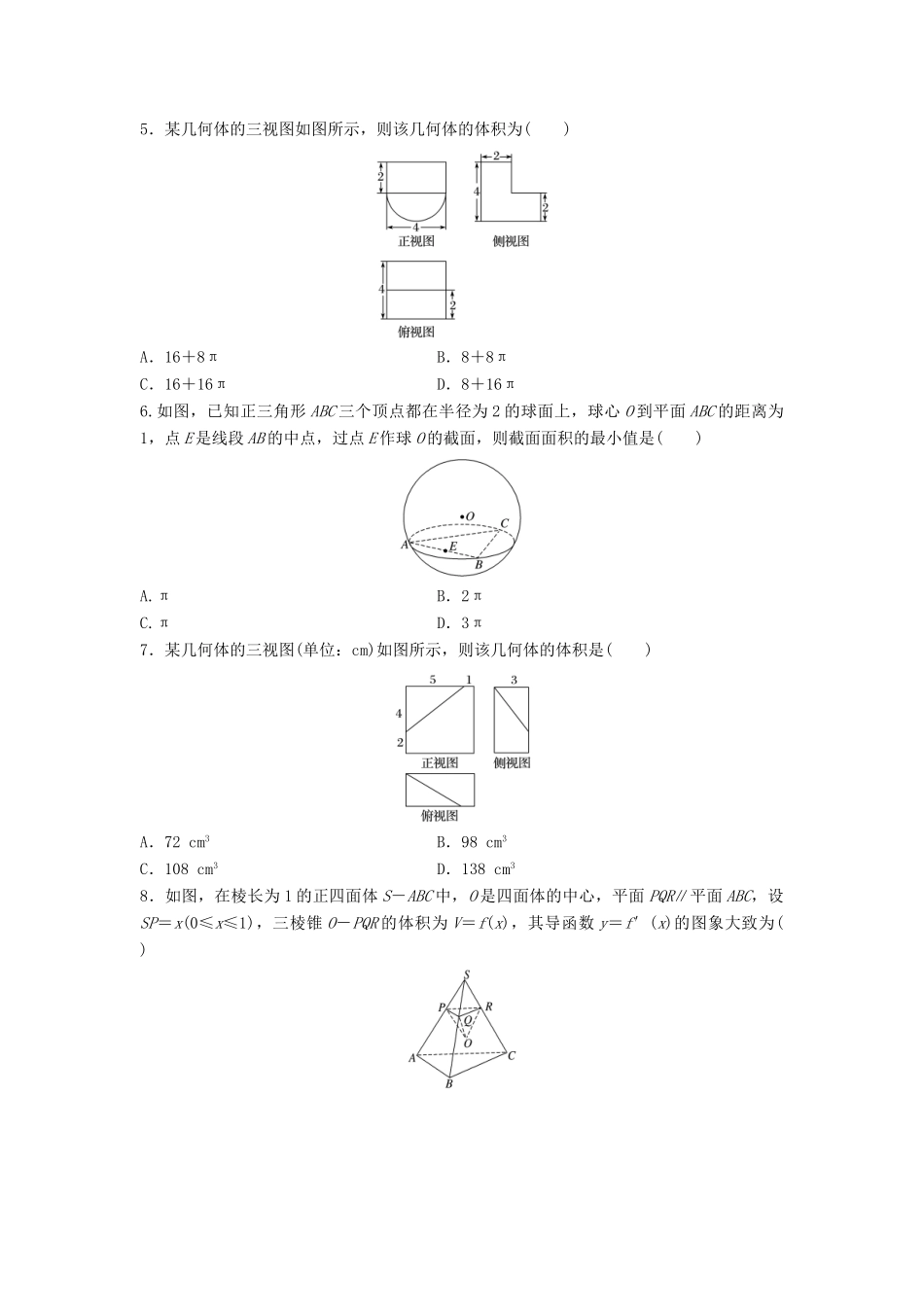
第50练表面积与体积训练目标(1)会利用几何体的表面积、体积公式求几何体的表面积、体积;(2)能通过几何体的三视图还原几何体,求面积、体积.训练题型(1)求简单几何体的表面积、体积;(2)求简单的组合体的表面积、体积;(3)通过三视图还原几何体求几何体的面积、体积.解题策略由三视图求面积、体积关键在于还原几何体,球的问题关键在确定球半径,不规则几何体可通过分割、补形转化为规则几何体求面积、体积.一、选择题1.在体积为的三棱锥S-ABC中,AB=BC=2,∠ABC=90°,SA=SC,且平面SAC⊥平面ABC,若该三棱锥的四个顶点都在同一球面上,则该球的体积是()A.B.C.D.12π2.如图是一个空间几何体的三视图,则该空间几何体的表面积是()A.(8+2)πB.(9+2)πC.(10+2)πD.(8+2)π3.(2016·山西四校联考)如图是一个几何体的三视图,则该几何体的表面积是()A.5+B.5+2C.4+2D.4+24.(2016·唐山模拟)若正三棱锥的高和底面边长都等于6,则其外接球的表面积为()A.64πB.32πC.16πD.8π5.某几何体的三视图如图所示,则该几何体的体积为()A.16+8πB.8+8πC.16+16πD.8+16π6.如图,已知正三角形ABC三个顶点都在半径为2的球面上,球心O到平面ABC的距离为1,点E是线段AB的中点,过点E作球O的截面,则截面面积的最小值是()A.πB.2πC.πD.3π7.某几何体的三视图(单位:cm)如图所示,则该几何体的体积是()A.72cm3B.98cm3C.108cm3D.138cm38.如图,在棱长为1的正四面体S-ABC中,O是四面体的中心,平面PQR∥平面ABC,设SP=x(0≤x≤1),三棱锥O-PQR的体积为V=f(x),其导函数y=f′(x)的图象大致为()二、填空题9.如图,在三棱柱A1B1C1-ABC中,D,E,F分别是AB,AC,AA1的中点,设三棱锥F-ADE的体积为V1,三棱柱A1B1C1-ABC的体积为V2,则V1∶V2=________.10.(2016·九江模拟)已知矩形ABCD的顶点都在半径为2的球O的球面上,且AB=3,BC=,过点D作DE垂直于平面ABCD,交球O于E,则棱锥E-ABCD的体积为________.11.如图,在长方体ABCD-A1B1C1D1中,AB=AD=3cm,AA1=2cm,则三棱锥A-B1D1D的体积为________cm3.12.已知球O的直径PQ=4,A,B,C是球O球面上的三点,△ABC是等边三角形,且∠APQ=∠BPQ=∠CPQ=30°,则三棱锥P-ABC的体积为________.答案精析1.B[如图,设球心为O,半径为R,取AC中点为M,连接SM,依据图形的对称性,点O必在SM上,由题设可知××2×2×SM=,解得SM=2,连接OC,则在Rt△OMC中,R2=(2-R)2+2,解得R=,则V=×()3=,故应选B.]2.A[从三视图所提供的图形信息和数据信息可知该几何体是一个圆锥和一个圆柱的组合体.圆柱的底面面积为π,侧面积为2π×1×2=4π,圆锥的底面积为4π,由于其母线长为,因此其侧面面积为×2π×2×=2π,故该几何体的表面积S=2π+4π+4π-π+π=(2+8)π,故选A.]3.A[该几何体的直观图如图.表面积S=1×1+×1×1×2+2××(1+2)×1+××=5+,所以选A.]4.A[如图,作PM⊥平面ABC于点M,则球心O在PM上,PM=6,连接AM,AO,则OP=OA=R(R为外接球半径),在Rt△OAM中,OM=6-R,OA=R,又AB=6,且△ABC为等边三角形,故AM==2,则R2-(6-R)2=(2)2,解得R=4,则球的表面积S=4πR2=64π.]5.A[由三视图可知,该组合体下半部分是一个半圆柱,上半部分是一个长方体,故体积V=2×2×4+×π×22×4=16+8π.]6.C[所作的截面与OE垂直时,截面圆的面积最小,设正三角形ABC的高为3a,则4a2+1=4,即a=,此时OE2=12+=.截面圆半径r2=22-=,故截面面积为.]7.B[该几何体的体积V=V长方体-V三棱柱=6×6×3-××3×4×5=98(cm3).]8.A[设O点到底面PQR的距离为h,即三棱锥O-PQR的高为h,设底面PQR的面积为S,∴三棱锥O-PQR的体积为V=f(x)=Sh,点P从S到A的过程中,底面积S一直在增大,高h先减小再增大,当底面经过点O时,高为0,∴体积先增大,后减小,再增大,故选A.]9.1∶24解析设三棱锥F-ADE的高为h,则==.10.2解析如图所示,BE过球心O,∴DE==2,∴VE-ABCD=×3××2=2.11.3解析×B1A1=××AD×D1D×B1A1=××3×2×3=3.12.解析如图,设球心为M,△ABC截面所截小圆的圆心为O.∵△ABC是等边三角形,∠APQ=∠BPQ=∠CPQ=30°,∴P在平面ABC上的投影是△ABC的中心O.设AB的中点为H,∵PQ是直径,∴∠PCQ=90°,∴PC=4cos30°=2,∴PO=2cos30°=3,OC=2sin30°=.∵O是△ABC的中心,∴OC=CH,∴△ABC的高CH=,AC==3,∴V三棱锥P-ABC=PO·S△ABC=×3×××3=.