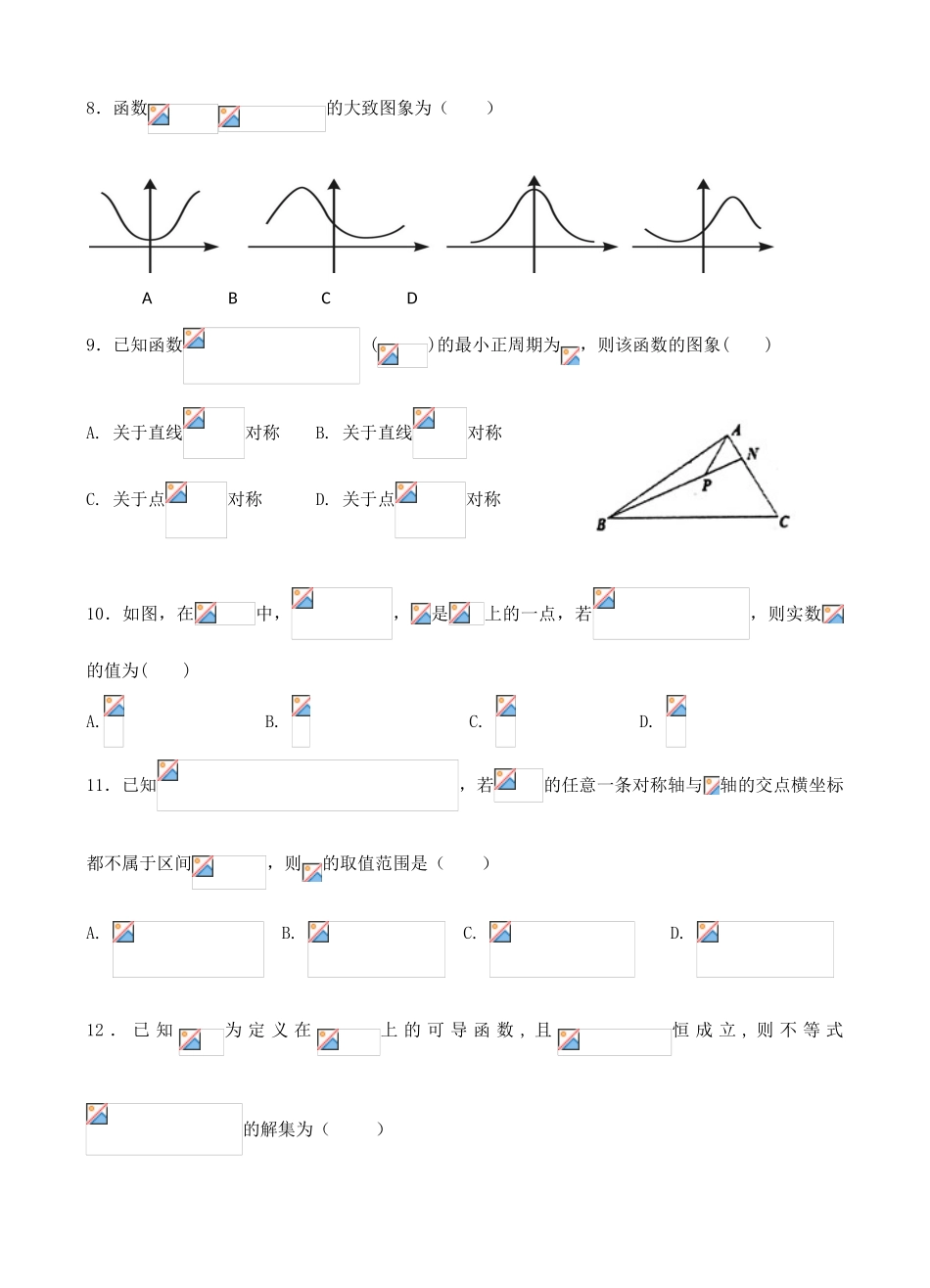
福建省南安市2018届高三数学上学期暑假期初考试(8月)试题理第Ⅰ卷(选择题共60分)一、选择题(本大题共12小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的)1.设集合,,,则()A.B.C.D.2.已知命题“”,则为()A.B.C.D.3.已知角的终边经过点,则的值是()A.或B.或C.或D.4.“”是函数“的最小正周期为”的()A.充分而不必要条件B.必要而不充分条件C.充要条件D.既不充分也不必要条件5.设,则的大小关系是()A.B.C.D.6.为了得到函数的图象,可以将函数的图象()A.向右平移个单位B.向左平移个单位C.向右平移个单位D.向左平移个单位7.已知向量满足,且,则与的夹角为()A.B.C.D.8.函数的大致图象为()9.已知函数()的最小正周期为,则该函数的图象()A.关于直线对称B.关于直线对称C.关于点对称D.关于点对称10.如图,在中,,是上的一点,若,则实数的值为()A.B.C.D.11.已知,若的任意一条对称轴与轴的交点横坐标都不属于区间,则的取值范围是()A.B.C.D.12.已知为定义在上的可导函数,且恒成立,则不等式的解集为()ABCDA.B.C.D.第Ⅱ卷(非选择题共90分)二、填空题(本大题共小题,每小题5分,共20分.把答案填在答题卡相应位置)13已知向量则.14已知,,则=________.15.已知在中,,,其外接圆的圆心为,则________.16.已知的三个内角所对的边分别为,且,则面积的最大值为.三、解答题(本大题共6小题,共70分.解答应写出文字说明、证明过程或演算步骤)17、(本小题满分12分)已知函数,(其中)的图象与轴的交点中,相邻两个交点之间的距离为,且图象上一个最低点为.(Ⅰ)求函数的解析式并确定函数对称中心;(Ⅱ)当时,求的最值.18、(本小题满分12分)中,角A,B,C的对边分别为,且(Ⅰ)求角B的大小;(Ⅱ)若,求的值.19、(本小题满分12分)已知函数(Ⅰ)当时,求的最小值;(Ⅱ)若函数在区间(0,1)上为单调函数,求实数的取值范围.20、(本小题满分12分)在中,,点在边上,,且.(Ⅰ)若△的面积为,求;(Ⅱ)若,求.21、(本小题满分12分)已知函数,其中为自然对数的底数.(Ⅰ)若曲线在处的切线与曲线在处的切线互相垂直,求实数的值;(Ⅱ)设函数,试讨论函数零点的个数.选考题,任选一题作答,两题只选一题做.22.(本小题满分10分)选修4-4:极坐标系与参数方程在直角坐标系中,直线的参数方程为(为参数),在以O为极点,轴正半轴为极轴的极坐标系中,曲线的极坐标方程为(Ⅰ)求直线的普通方程与曲线的直角坐标方程;(Ⅱ)若直线与轴的交点为,直线与曲线的交点为,求的值.23.(本小题满分10分)选修4-5:不等式选讲设.(Ⅰ)若的解集为,求实数的值;(Ⅱ)当时,若存在,使得不等式成立,求实数的取值范围.南安一中2018届高三数学(理)暑期试卷2017.8.28参考答案一、选择题123456789101112DCDAADBCDACB二、填空题(13)2;(14)-26(15)10(16)17、解:(Ⅰ)由已知得即所以…………………1分又因为图象上一个最低点为所以且…………………2分所以即()又因为所以…………………3分所以…………………4分由得()所以函数对称中心为()…………………-6分(Ⅱ)由得所以…………………9分所以的最大值为,此时;的最小值为,此时…………………12分18解:(Ⅰ),由正弦定理,得,…………………2分…………………4分因为,所以,所以,因为,所以.…………………6分(Ⅱ)三角形中,,,所以…………………8分………10分.…………………12分19、解:(Ⅰ)已知函数,所以定义域为:;所以令,得的增区间为;令,得的减区间为(0,1),所以的最小值为。…………………6分(Ⅱ)求导得:,定义域为:,则对讨论。因在(0,1)上为单调函数,即求在(0,1)上恒大于0或恒小于0;配方得,对称轴为,开口向上,在区间(0,1)上为增函数,若函数在(0,1)上为单调增函数,即,只需,得;若函数在(0,1)上为单调减函数,即,得,综上得:。…………………12分20、解法一:(Ⅰ)因为,即,…………………2分又因为,,所以.…………………3分在△中,由余弦定理得,,…………………5分即,解得.…………...