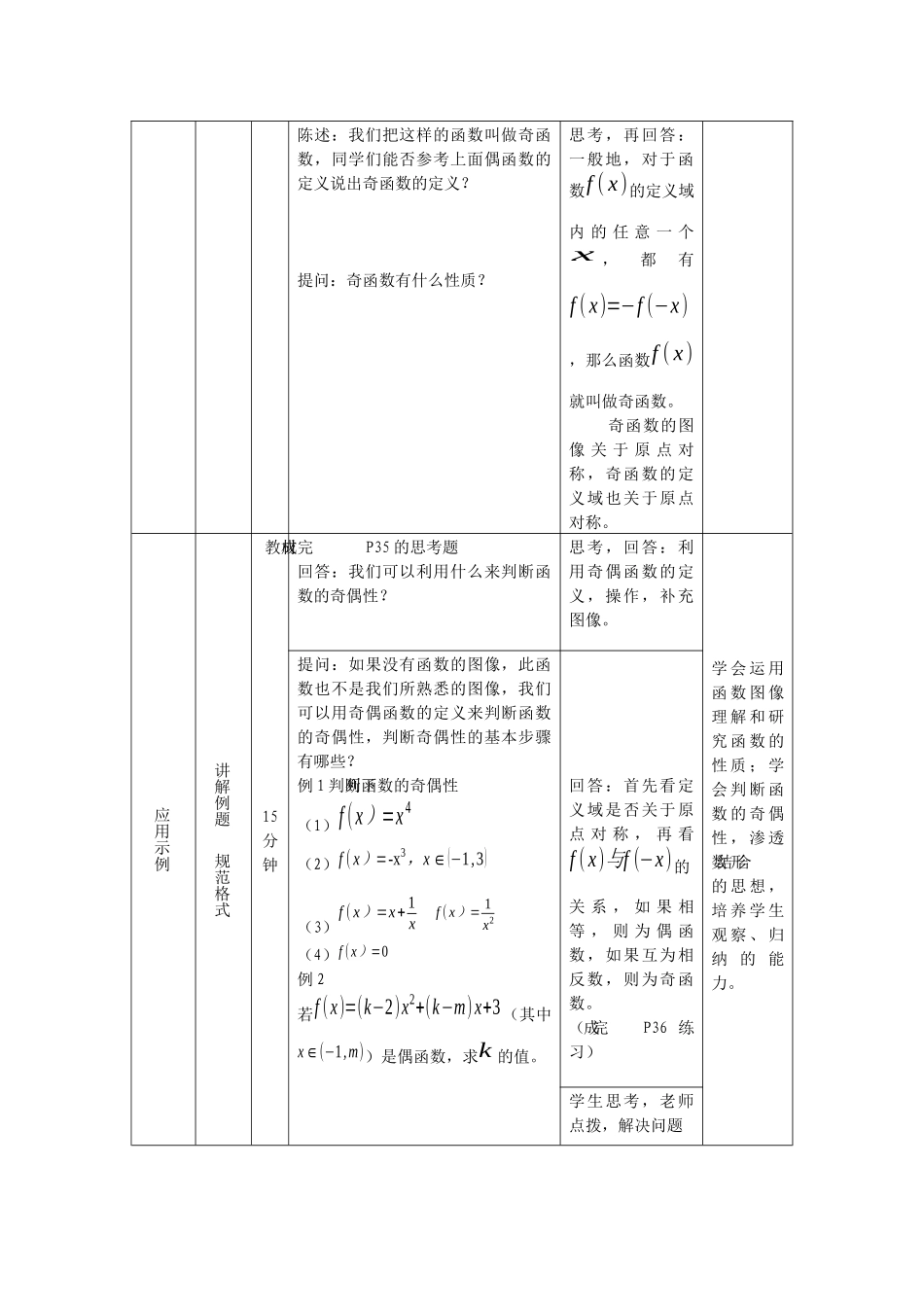
教学内容教学环节活动时间《函数奇偶性》教学设计设计意图教师活动学生活动课题引入创设情境2分钟陈述:前面学习了函数的单调性,它是反映函数在某个区间上函数值随自变量变化而变化的性质,今天我们继续研究函数的另一个性质,从什么角度研究呢?在现实生活中,我们有过许多对称美的感受,你能举出“对称美”的例子吗?学生思考回答提出实际情境,引发学生思考。设疑激趣提出问题3分钟由于函数是用来揭示自然界奥秘的,因此有些函数便天然的具有这种对称性。那么此时的函数具有哪些性质呢?这些性质能否给我们带来美的享受呢?我们首先来看看我们所熟悉的几个函数的图像:y=x2,y=|x|(观察后)回答:两个函数图像都是对称的,而且都是关于y轴对称。提出问题,培养学生观察、归纳、抽象的能力。观察图像,完成表格,回答下面两个问题。(填表后)回答:自变量取一对相反数时,函数值是相等的。f(x)=f(−x)提问:(1)这两个图像有什么共同的特征?(2)相应的两个函数值对应表是如何体现这些特征的?(3)如果对于任意的自变量,怎么表示这种特征?新课探究指导观察形成概念10分钟陈述:我们把像y=x2这样的函数称做偶函数。给出偶函数的定义:一般地,对于函数f(x)的定义域内的任意一个x,都有f(x)=f(−x),那么函数f(x)就叫做偶函数。观察,思考了解偶函数的定义和t图像性质,为后面的奇函数铺垫。提问:从偶函数的定义来看,偶函数有什么性质?回答:偶函数的图像关于y轴对称,偶函数的定义域也关于原点对称。陈述:观察y=x,y=1x的图像,完成书上P34的表格,回答下面两个问题:这两个函数有什么共同特征。相应的两个函数值对应表如何体现这些特征?观察、思考,回答:两个函数图像都关于原点对称,当自变量x取一对相反数时,相应的函数值f(x)也是一对相反数。归纳:对于任意的x,都有f(x)=−f(−x)陈述:我们把这样的函数叫做奇函数,同学们能否参考上面偶函数的定义说出奇函数的定义?提问:奇函数有什么性质?思考,再回答:一般地,对于函数f(x)的定义域内的任意一个x,都有f(x)=−f(−x),那么函数f(x)就叫做奇函数。奇函数的图像关于原点对称,奇函数的定义域也关于原点对称。应用示例讲解例题规范格式15分钟完成教材P35的思考题回答:我们可以利用什么来判断函数的奇偶性?思考,回答:利用奇偶函数的定义,操作,补充图像。学会运用函数图像理解和研究函数的性质;学会判断函数的奇偶性,渗透数形结合的思想,培养学生观察、归纳的能力。提问:如果没有函数的图像,此函数也不是我们所熟悉的图像,我们可以用奇偶函数的定义来判断函数的奇偶性,判断奇偶性的基本步骤有哪些?例1判断下列函数的奇偶性(1)f(x)=x4(2)f(x)=-x3,x∈(−1,3)(3)f(x)=x+1xf(x)=1x2(4)f(x)=0例2若f(x)=(k−2)x2+(k−m)x+3(其中x∈(−1,m))是偶函数,求k的值。回答:首先看定义域是否关于原点对称,再看f(x)f与(−x)的关系,如果相等,则为偶函数,如果互为相反数,则为奇函数。(完成P36练习)学生思考,老师点拨,解决问题巩固练习课堂练习加深理解7分钟[练习]下列命题正确的是()A偶函数一定与y轴相交B奇函数图像一定经过原点C不存在既是奇函数又是偶函数的函数D既不是奇函数又不是偶函数的函数是存在的定义在R上的奇函数f(x)一定满足的关系式()Af(x)−f(−x)>0Bf(x)−f(−x)<0Cf(x)⋅f(−x)≥0Df(x)⋅f(−x)≤0(3)若f(x)=ax2+bx+c(a≠0)是偶函数,则g(x)=ax3+bx2+cx是()A奇函数B偶函数C非奇非偶函数D奇函数或偶函数(4)已知f(x)为[−1,1]上的奇函数,则f(1)+f(0)+f(−1)的值为______(5)已知y=f(x)是奇函数,当x<0时,f(x)=x2+ax,且f(3)=6,则a的值为______巩固新知加深理解(6)已知y=f(x)=3ax3+4bx+3a+b是奇函数,且其定义域为[2a−6,a],则a=_____b=_____。(7)下图只画了函数图像的一部分,请根据函数的奇偶性补全图形。f(x)是偶函数f(x)是奇函数(8)如图给出了奇函数y=f(x)的局部图像,求f(−4)的值,写出f(x)的单调区间,并比较f(−1)与f(−3)的大小。(9)函数f(x)是定义域为实数集xy011R的偶函数,它在区间[0,+∞)上是增函数,若有:f(m)...