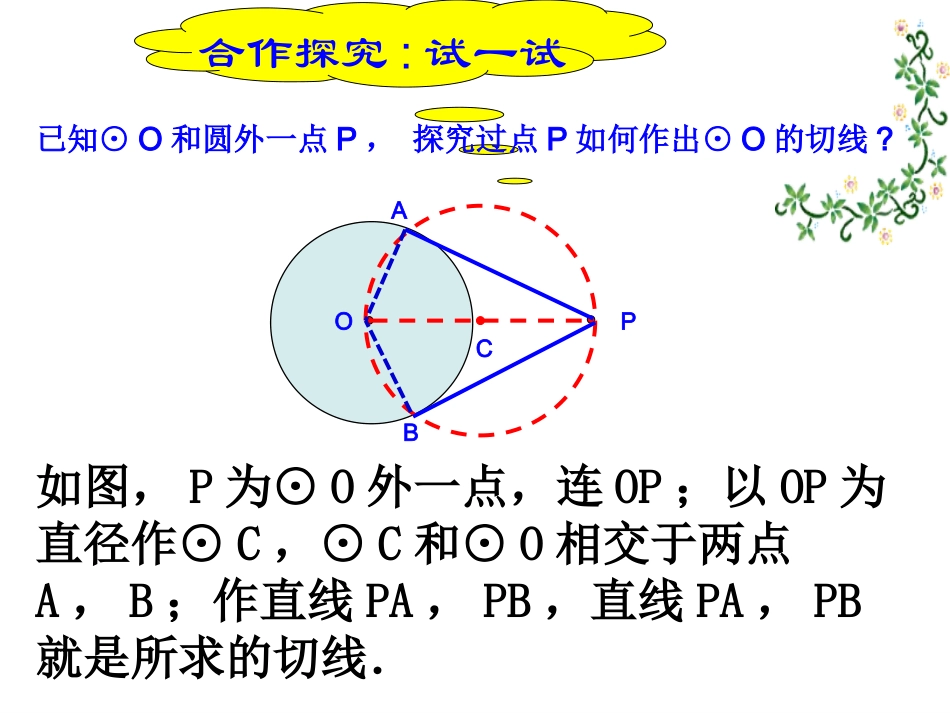
2.直线与圆的位置关系(四)24.2与圆有关的位置关系我们可以知道,过⊙O上任一点A都可以作一条切线,并且只有一条,根据下面提出的问题操作思考并解决这个问题.过圆外一点P能否作圆的切线?如果能,能作几条?如何作?(一)问题探究过一点作圆的切线,能作几条?合作探究:试一试PO已知⊙O和圆外一点P,探究过点P如何作出⊙O的切线?BA如图,P为⊙O外一点,连OP;以OP为直径作⊙C,⊙C和⊙O相交于两点A,B;作直线PA,PB,直线PA,PB就是所求的切线.C(二)建立概念经过圆外一点作圆的切线,这点和切点之间的线段的长,叫做这点到圆的切线长.切线和切线长是两个不同的概念,切线是直线,不能度量;切线长是线段的长,这条线段的两个端点分别是圆外一点和切点,可以度量.OBAP(三)探索结论若从⊙O外的一点P引两条切线PA,PB,切点分别是A、B,连结OA、OB、OP,你能发现什么结论?并证明你所发现的结论。利用切线的性质得∠PAO=∠PBO=90°,易证RtAPORtPBO△≌△,得到PA=PB,∠1=∠2,21OBAP用文字语言叙述你发现的结论:21OBAP切线长定理从圆外一点引圆的两条切线,它们的切线长相等,圆心和这一点的连线平分两条切线的夹角.定理的几何符号表达: PA、PB分别切⊙O于A、B,∴PA=PB,∠1=∠2反思:切线长定理为证明线段相等、角相等提供了新的方法。(四)研究图形下面我们对切线长定理的基本图形作进一步的研究。如图,P是⊙O外一点,PA,PB是⊙O的两条切线,直线OP交⊙O于D、E,交弦AB于C,87654321DOPECBA(1)写出图中所有的相等关系;(2)写出图中所有的垂直关系;(3)写出图中所有的全等三角形.87654321DOPECBA由以上探索可知:切线长定理为证明线段相等,角相等,弧相等,垂直关系等等提供了新的依据,必须掌握并灵活应用。(1)相等关系:PA=PB,AC=BC,OA=OB,AD=BD,∠1=2=3=4∠∠∠,∠5=6∠=∠7=∠8,弧AD=弧BD,弧AE=弧BE,(2)垂直关系:OAAP⊥,OBBP⊥,OPAB⊥.(3)全等三角形:△PACPBC≌△,△ACOBCO≌△,△PAOPBO≌△.例1圆的外切四边形ABCD,四边与圆的切点分别为E、F、G、H(1)图中有哪些相等的线段(2)猜想四边形的两组对边怎样的关系反思:圆的外切四边形的两组对边的和相等。(五)定理应用练习:四边形ABCD外切于⊙O(1)若AB:BC:CD:DA=2:3:n:4则n=____(2)若AB:BC:CD=5:4:7,周长为48,则最长的边为_____·ABCDO516例2如图,从⊙O外一点P作⊙O的两条切线,分别切⊙O于A、B,在弧AB上任取一点C作⊙O的切线分别交PA、PB于D、E,QOEDCBAP(1)若PA=2,则△PDE的周长为;若PA=a,则△PDE的周长为____。42a例2如图,从⊙O外一点P作⊙O的两条切线,分别切⊙O于A、B,在弧AB上任取一点C作⊙O的切线分别交PA、PB于D、E,QOEDCBAP(2)连结OD、OE,Q为优弧AB上任一点,若∠P=40°,则∠DOE=_____,∠Q=____;若∠P=α,∠DOE=_______,∠Q=______。70°70°902902变式练习如图,从⊙O外一点P作⊙O的两条切线,若C为弧AB上一动点,过C作⊙O的切线分别交PA、PB于D、E,Q为优弧AB上任一点,求证:①△PDE的周长为定值,并求出定值;②∠DOE的度数为定值,并求出定值,③你发现∠DOE和∠Q有怎样的关系,并证明你的结论。QOEDCBAP例3如图,AB是⊙O的直径,AD、BC、CD分别切⊙O于A、B、E,若BC=9,AD=4,求OE的长。方法1:连接OD,OC,利用切线长定理,OD平分∠ADC,OC平分∠BCD,易得DO⊥CO,根据Rt△ADO,Rt△DEO,Rt△CEO,利用勾股定理建立关于r的方程:222224949rr得r=6。FEDCBAO在Rt△DCF中,由勾股定理得方程:2222513r,得r=6。方法2:作DF⊥BC于F,易证四边形ABFD为矩形,AD=BF=4,DF=AB,设OE=OA=OB=r,则CF=BC-BF=5,DF=AB=2r,CD=CE+DE=BC+AD=13,变式练习一如图,⊙O的直径AB=12cm,AD、BC、CD分别切⊙O于A、B、E,设AD=x,BC=y.求y与x的函数关系式,并说明是什么函数?答案:,是反比例函数。36yx变式练习二已知O是正方形ABCD一边BC的中点,AP与以O为圆心,OB为半径的圆切于T点,求AT:TP的值。TPODCBA,求得x:y=4:1。基于本题有正方形这一条件,还可这样解决:如图,...