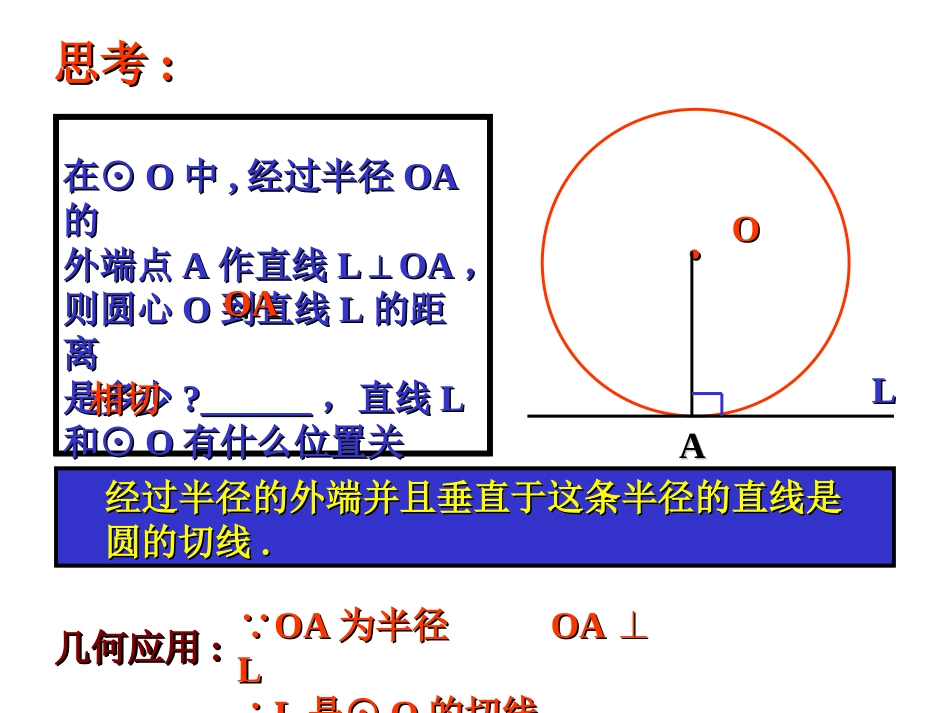
2.直线与圆的位置关系(二)24.2与圆有关的位置关系复习1.直线和圆有哪些位置关系?2.什么叫相切?3.我们学习过哪些切线的判断方法?在⊙在⊙OO中中,,经过半径经过半径OAOA的的外端点外端点AA作直线作直线LOA⊥LOA⊥,,则圆心则圆心OO到直线到直线LL的距的距离离是多少是多少?______?______,直线,直线LL和⊙和⊙OO有什么位置关有什么位置关系系??_________._________.思考思考::..OOAAOAOA相切相切LL经过半径的外端并且垂直于这条半径的直线是经过半径的外端并且垂直于这条半径的直线是圆的切线圆的切线..几何应用几何应用:: OAOA为半径为半径OAOA⊥⊥LL∴∴LL是⊙是⊙OO的切线的切线几何应用几何应用::判断1.过半径的外端的直线是圆的切线()2.与半径垂直的的直线是圆的切线()3.过半径的端点与半径垂直的直线是圆的切线()××××××OOrrllAAOOrrllAAOOrrllAA利用判定定理时,要注意直线须具备以利用判定定理时,要注意直线须具备以下两个条件下两个条件,,缺一不可缺一不可::(1)(1)直线经过半径的外端直线经过半径的外端;;(2)(2)直线与这半径垂直。直线与这半径垂直。判断一条直线是圆的切线,你现在会有判断一条直线是圆的切线,你现在会有多少种方法多少种方法??有以下三种方法有以下三种方法::(1)(1)利用切线的定义利用切线的定义::与圆有唯一公共点的直与圆有唯一公共点的直线是圆的切线。线是圆的切线。(2)(2)利用利用dd与与rr的关系作判断的关系作判断::当当dd==rr时直时直线是圆的切线。线是圆的切线。(3)(3)利用切线的判定定理利用切线的判定定理::经过半径的外端并经过半径的外端并且垂直于这条半径的直线是圆的切线。且垂直于这条半径的直线是圆的切线。想一想其中(2)和(3)本质相同,只是表达形式不同.解题时,灵活选用其中之一.例1已知:直线AB经过⊙O上的点C,并且OA=OB,CA=CB。求证:直线AB是⊙O的切线。OOBBAACC分析:由于AB过⊙O上的点C,所以连接OC,只要证明AB⊥OC即可。证明:连结OC(如图) OA=OB,CA=CB,∴OC是等腰三角形OAB底边AB上的中线。∴AB⊥OC。 OC是⊙O的半径∴AB是⊙O的切线。例例22已知:已知:OO为∠为∠BACBAC平分线上一平分线上一点,点,OD⊥ABOD⊥AB于于D,D,以以OO为圆心,为圆心,ODOD为半径作⊙为半径作⊙OO。。求证:⊙求证:⊙OO与与ACAC相切。相切。OOAABBCCEEDD证明:过O作OE⊥AC于E。 AO平分∠BAC,OD⊥AB∴OE=OD OD是⊙O的半径∴O到AC的距离等于半径∴AC是⊙O的切线。小结例1与例2的证法有何不同?(1)如果已知直线经过圆上一点,则连结这点和圆心,得到辅助半径,再证所作半径与这直线垂直。简记为:连半径,证垂直。(2)如果已知条件中不知直线与圆是否有公共点,则过圆心作直线的垂线段为辅助线,再证垂线段长等于半径长。简记为:作垂直,证半径。OOBBAACCOOAABBCCEEDD练习如图,△如图,△AOBAOB中,中,OAOA==OBOB==1010,∠,∠AOBAOB==120°120°,以,以OO为圆心,为圆心,55为半径的⊙为半径的⊙OO与与OAOA、、OBOB相交。相交。求证:求证:ABAB是⊙是⊙OO的切线。的切线。OOBBAACC证明:连结OP。 AB=AC,∴∠B=∠C。 OB=OP,∴∠B=∠OPB,∴∠OPB=∠C。∴OP∥AC∴∠OPE=∠PEC PE⊥AC,∴∠PEC=90°∴∠OPE=90°∴PE⊥OP。 OP是半径∴PE为⊙0的切线。如图如图,△ABC,△ABC中,中,AB=ACAB=AC,以,以ABAB为直径的⊙为直径的⊙OO交边交边BCBC于于PP,,PE⊥ACPE⊥AC于于EE。。求证求证:PE:PE是⊙是⊙OO的切线。的切线。练习OOAABBCCEEPP例3如图,△ABC内接于⊙O,AB为直径,∠CAE=∠B,求证:AE是⊙O的切线。EOCBA例4如图,AB是⊙O的直径,点D在AB的延长线上,BD=OB,点C在圆上,∠CAB=30°,求证:DC是⊙O的切线。ODCBA例5如图,AB是⊙O的直径,D是弧BC的中点,DE⊥AC的延长线于E,求证:DE是⊙O的切线。例6如图,△APC内接于⊙O,AB是⊙O的直径,且∠EAC=∠P。求证:AE是⊙O的切线。12例7如图,在Rt△ABC中,∠B=90°,∠A的平分线交BC于点D,E为AB上一点,DE=DC,以D为圆心,DB长为半径作⊙D,求证:(1)AC是⊙D的切线;(2)AB+EB=AC。F课堂小结1.判定切线的方法有哪些?直线l与圆有唯一公共...