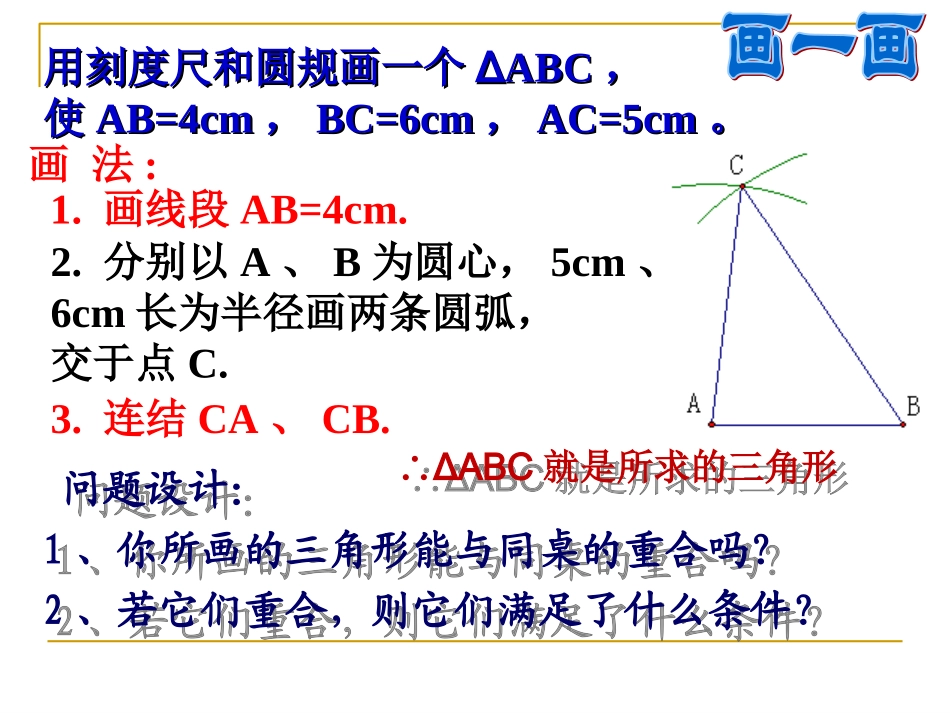
12.2三角形全等的判定(一)授课人:授课人:大悟县城关中学大悟县城关中学胡玉霞胡玉霞12.2三角形全等的判定(一)授课人:授课人:大悟县城关中学大悟县城关中学胡玉霞胡玉霞1.怎样的两个三角形是全等三角形?2.两个全等三角形具有怎样的性质?EFGABC3.两个三角形需满足几个条件才能说明它们全等?能否只取一部分条件来判断两个三角形全等?全等三角形的对应边相等,对应角相等全等三角形的对应边相等,对应角相等完全重合的两个三角形全等完全重合的两个三角形全等用刻度尺和圆规画一个用刻度尺和圆规画一个ΔΔABCABC,,使使AB=4cmAB=4cm,,BC=6cmBC=6cm,,AC=5cmAC=5cm。。1.画线段AB=4cm.画法:2.分别以A、B为圆心,5cm、6cm长为半径画两条圆弧,交于点C.3.连结CA、CB.问题设计:1、你所画的三角形能与同桌的重合吗?2、若它们重合,则它们满足了什么条件?问题设计:1、你所画的三角形能与同桌的重合吗?2、若它们重合,则它们满足了什么条件?∴ΔABC就是所求的三角形∴ΔABC就是所求的三角形三边对应相等的两个三角形全等(简写成“边边边”或“SSS”)ABCA′B′C′AB=A'B'(已知)AC=A'C'(已知)BC=B'C'(已知)∴△ABCA≌△'B'C'(SSS)在△ABC和△A'B'C'中证明:在△ABC和△DCB中:AB=DC()∵AC=DB()=()证明:在△ABC和△DCB中:AB=DC()∵AC=DB()=()∴△ABC≌()∴△ABC≌()BCBCCBCB△DCB△DCBAABBCCDD练习:练习:已知已知如图,AB=CD,AC=BD,求证:△ABC≌△DCB如图,AB=CD,AC=BD,求证:△ABC≌△DCB已知已知公共边公共边SSSSSS例1、如图△ABC是一个钢架,AB=AC,AD是连结点A和BC中点D的支架,求证:△ABD△ACD≌ABCD证明:∵D是BC的中点∴BD=CD在△ABD和△ACD中,AB=AC(已知)AD=AD(公共边)DB=DC∴△ABD△ACD△(SSS)例2、如图,已知AB=CD,AD=CB,试说明∠B=∠D的理由解:连结AC∴∠B=∠D(全等三角形对应角相等)ABCDABCDAB=CD(已知)AC=CA(公共边)CB=AD(已知)∴△ABCCDA≌△(SSS)在△ABC和△CDA中小结:要说明两个角相等,可以利用它们所在的两个三角形全等的性质来说明。能说明∠A=∠C吗?辅助线:有时为了解题需要,在原图形上添一些线,这些线叫做辅助线。辅助线通常画成虚线.练习:如图,已知点B、E、C、F在同一条直线上,AB=DE,AC=DF,BE=CF。试说明∠A=∠D的理由。∵BE=CF(已知)即BC=EF在△ABC和△DEF中AB=DE(已知)AC=BF(已知)BC=EF(已证)∴△ABCDEF≌△(SSS)∴∠A=∠D(全等三角形对应角相等)FABECD∴BE+EC=CF+EC解:证明:∵BD=CE∴BD-ED=CE-ED,即BE=CD。CABDE在△AEB和△ADC中,AB=AC(已知)AE=AD(已知)BE=CD(已证)∴△AEB≌ADC△(sss)1:如图,AB=AC,AE=AD,BD=CE,求证:△AEB≌△ADC。2:已知:如图.AB=DC,AC=DB,求证:∠A=D∠ABDCo1、“SSS”公理及其应用。2、证角(或线段)相等转化为证角(或线段)所在的三角形全等;3、四边形问题转化为三角形问题来解决。课堂小结:谢谢