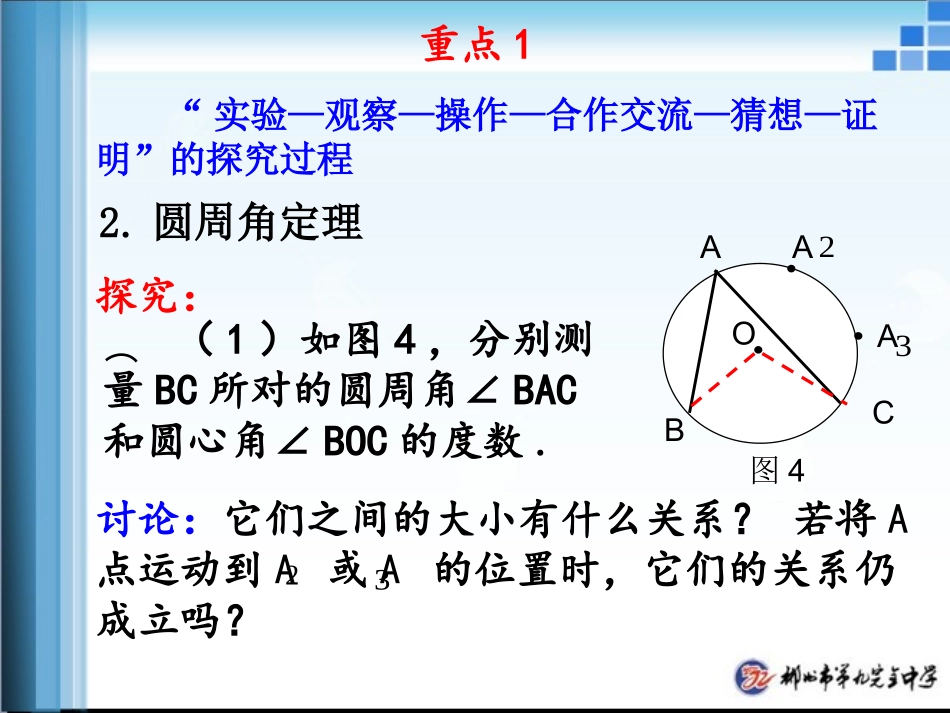
圆周角与圆心角及其所对弧的关系前面学习了圆周角的定义,下面就进入圆周角定理的探索和证明过程。2.圆周角定理探究:(1)如图4,分别测量BC所对的圆周角∠BAC和圆心角∠BOC的度数.32讨论:它们之间的大小有什么关系?若将A点运动到A或A的位置时,它们的关系仍成立吗?重点1“实验—观察—操作—合作交流—猜想—证明”的探究过程B图4CAOA2A3实验:每位同学任画一个圆,并在圆上任取一条弧,作出这条弧所对的圆周角和圆心角,测量它们的度数,你能得出同样的结论吗?通过测量,我们发现:圆周角的度数等于它所对的弧所对的圆心角的度数的一半。分析:由于猜想的结论是由有限个度量结果得出的,而BC所对的圆周角却有无数个,所以我们必须证明对这无数个圆周角结论都成立。那么怎样证明这无数个圆周角的度数都等于圆心角度数的一半呢?观察(图4):并注意这无数个圆周角和圆心角O的位置关系。图4重点2圆周角度数定理的证明因此我们只要分别证明上述三种情况即可。①∠①∠BACBAC的一边经过圆心的一边经过圆心OO③③圆心圆心OO在∠在∠BACBAC的外部的外部②②圆心圆心OO在∠在∠BACBAC的内部的内部BCOA(P1或P4)③③BCA(P3)O②OBCA(P2)①①发现:这无数个圆周角与圆心的位置关系有以下三种:∴∠BOC=2∠A∵OA=OB∴∠A=∠B∴∠BOC=∠B+∠A当圆心O在圆周角(∠A)的一边(AC)上时,圆周角∠A与圆心角∠BOC的大小关系.∵∠BOC是△BAO的外角●OBAC即∠A=∠BOC211.首先考虑第一种情况:第二种情况:2.当圆心O在圆周角(∠BAC)的内部时,圆周角∠BAC与圆心角∠BOC的大小关系会怎样?过点A作直径AD.●OBACD∠BAD=∠BOD,21●OBAC即∠BAC=∠BOC21提示:能否转化为第一种情况?21∠CAD=∠COD∠BAD+∠CAD=∠BOD+∠COD2121=∠BOC21由第一种情况可得:第三种情况:3.当圆心O在圆周角(∠BAC)的外部时,圆周角∠BAC与圆心角∠BOC的大小关系会怎样?提示:能否也转化为第一种情况?过点A作直径AD.●O结论:同弧所对的圆周角等于它所对的圆心角的度数的一半.D∠BAD=∠BOD21BAC●OBAC即∠BAC=∠BOC2121∠CAD=∠COD,∠BAD-∠CAD=∠BOD-∠COD2121=(∠BOD-∠COD)21由第一种情况可得:郴州市第九完全中学郴州市东江湖莽山云海