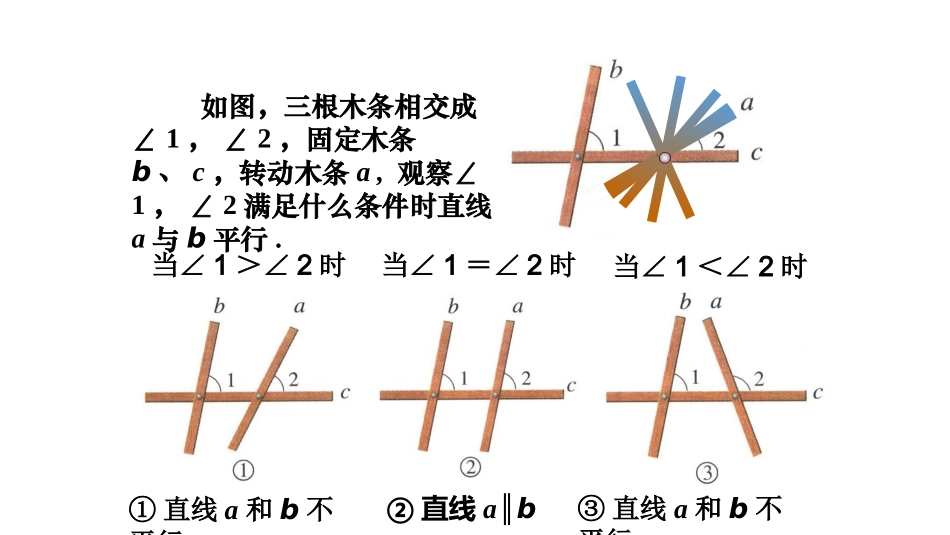
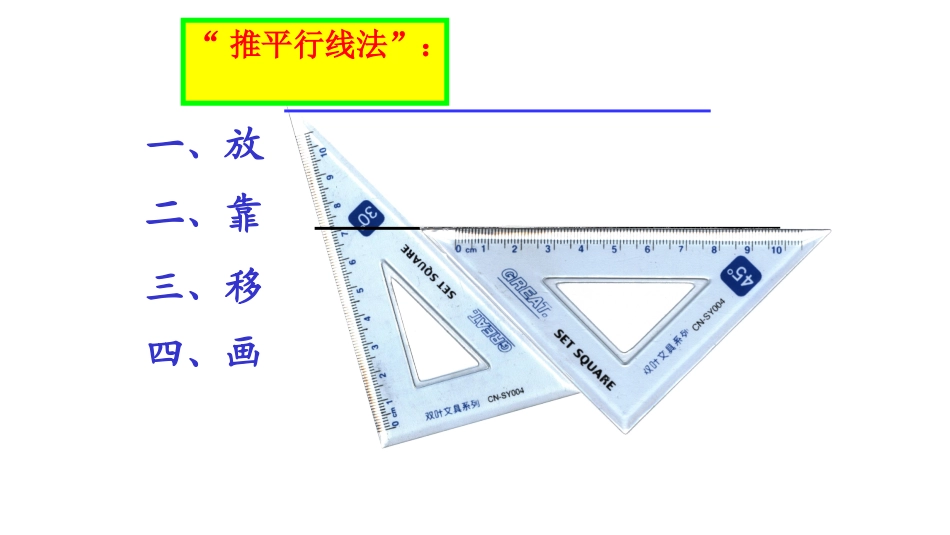
第1课时平行线的判定方法1湘教版七年级下册如图,三根木条相交成∠1,∠2,固定木条b、c,转动木条a,观察∠1,∠2满足什么条件时直线a与b平行.当∠1>∠2时当∠1=∠2时当∠1<∠2时①直线a和b不平行②直线a∥b③直线a和b不平行一、放二、靠三、移四、画“推平行线法”:请按图1-5所示方法画两条平行线,然后讨论下面的问题:(1)上面的画法可以看做是怎样的图形变换?1l2lAB(2)把图中的直线,看成被尺边所截,那么在画图过程中,什么角始终保持相等?由此你能发现画两直线平行方法的依据吗?1l2lAB两条直线被第三条直线所截,如果同位角相等,那么这两条直线平行.简单地说:同位角相等,两直线平行.∵∠1=2∠∴ABCD(∥同位角相等,两直线平行)推理形式BACDF12E1.已知直线l1,l2被l3所截,如图,∠1=45°,2∠=135°,试判断l1与l2是否平行.并说明理由.l3l1l2123l1∥l2,∠3=180°—2=45°=1∠∠随堂演练随堂演练2.如图,哪些直线平行,哪些直线不平行?l4l3l250°60°120°l1l3l∥4,l1与l2不平行,3.找出图中的平行线CADBEF如果∠ADE=ABC,∠则DEBC∥如果∠ACD=F,∠则DCBF∥如果∠DEC=BCF,∠则DEBC∥注:要确定是哪两条直线被第三条直线所截得到的同位角4.如图,已知∠ABD=∠ACE,BF、CG分别是∠ABD、∠ACE的平分线,请判断BF与CG是否平行,并说明理由。1ABCDEFG2平行,ABD=ACE,∵∠∠BF、CG分别是∠ABD、∠ACE的平分线∴∠1=2∠∴BFCE∥你学到了什么?你认为还有什么不懂的?你有什么经验与收获让同学们共享呢?课堂小结课堂小结1.同位角相等,两直线平行.2.内错角相等,两直线平行.3.同旁内角互补,两直线平行.4.如果两条直线都与第三条直线平行,那么这两条直线也互相平行.5.如果两条直线都与第三条直线垂直,那么这两条直线也互相平行.6.平行线的定义.判定两条直线是否平行的方法有:1.从课后习题中选取;2.完成练习册本课时的习题。课后作业课后作业第2课时平行线的判定方法2、3湘教版七年级下册如图,如果∠1=2∠,能得出AB∥CD吗?解:∵∠1=2∠(已知)∠1=3∠(对顶角相等)∴∠2=3∠∴ABCD∥(同位角相等,两直线平行)B1ACDF32E推进新课推进新课B12ADEF两条直线被第三条直线所截,如果内错角相等,那么这两条直线平行.C简单地说:内错角相等,两直线平行.∵∠1=2∠∴ABCD(∥内错角相等,两直线平行)推理形式如图,若∠4+2=180°∠,能得出AB∥CD吗?解:4+2=180°∵∠∠(已知)∠4+3=180°∠(补角的定义)∴∠2=3∠(同角的补角相等)∴ABCD∥(同位角相等,两直线平行)1AC3425DBEF你还有其它的说理方法吗?如图,如果∠4+2=180°∠,能得出AB∥CD?思考解∵∠4+2=180°∠(已知)∠4+1=180°∠(补角的定义)∴∠2=1∠(同角的补角相等)∴ABCD∥(内错角相等,两直线平行)1AC3425DBEF两条直线被第三条直线所截,如果同旁内角互补,那么这两条直线平行.2BACDEF1简单地说:同旁内角互补,两直线平行.∵∠1+2=180∠0∴ABCD(∥同旁内角互补,两直线平行)推理形式1.如图,∠B=40°,∠DFC=140°,试判断AB与DE是否平行,并说明理由。ABCDEF典例剖析典例剖析ABDE∥理由:∵∠BFE=∠DFC=140°∴∠BFE+∠B=180°∴ABDE∥