不同增长函数的差异VIP免费

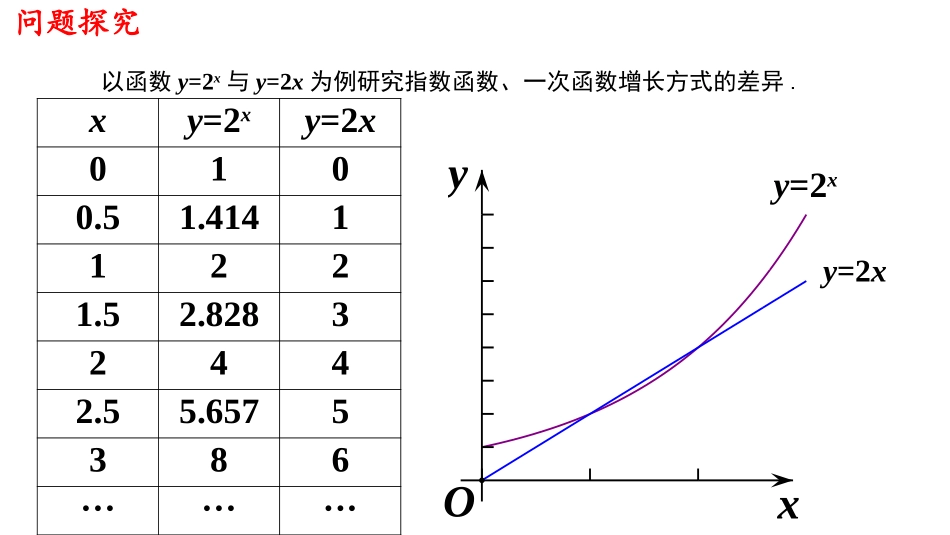
4.4.3不同增长函数的差异一次函数、指数函数、对数函数增长方式存在很大差异，这种差异正是不同类型现实问题具有不同增长规律的反映.下面就来研究一次函数f(x)=kx+b，k>0，指数函数g(x)=ax(a>1)，对数函数在定义域内增长方式的差异.log1ahxxa问题探究以函数y=2x与y=2x为例研究指数函数、一次函数增长方式的差异.xy=2xy=2x0100.51.41411221.52.82832442.55.6575386·········xyOy=2xy=2x问题探究探究1观察两个函数的交点坐标函数y=2x与y=2x有两个交点(1,2)和(2,4)探究2分别在区间(0,1)、(1,2)、(2,3)上，讨论函数y=2x的图象与y=2x的图象的关系？综上：函数y=2x的增长速度不变，但是y=2x的增长速度改变，先慢后快.xy(2,4)(1,2)1212345678O问题探究探究3请大家想象一下，取更大的x值，在更大的范围内两个函数图象的关系？尽管在x的一定范围内，2x<2x，但由于y=2x的增长最终会快于y=2x的增长，因此，总会存在一个x0，当x>x0时，恒有2x>2x.问题探究xy(2,4)(1,2)1212345678O归纳总结探究4指数函数y=ax(a>1)与一次函数y=kx(k>0)的增长情况如何呢？即使k值远远大于a值，指数函数y=ax(a>1)虽然有一段区间会小于y=kx(k>0)，但总会存在一个x0，当x>x0时，y=ax(a>1)的增长速度会大大超过y=kx(k>0)的增长速度.1．四个变量y1，y2，y3，y4随变量x变化的数据如表：x151015202530y1226101226401626901y22321024377681.05×1063.36×1071.07×109y32102030405060y424.3225.3225.9076.3226.6446.907关于x呈指数函数变化的变量是________.跟踪训练xy=lgx0不存在01011201.3012301.4773401.6024501.6995601.7786·········以函数y=lgx与为例研究对数函数、一次函数增长方式的差异.110yx110yxxy102030405060123456O110yxy=lgx问题探究观察两个函数图象及其增长方式：在(0,+∞)上增长速度不变，y=lgx在(0,+∞)图象越来越平缓，就像与x轴平行一样.110yxxy102030405060123456O110yxy=lgx问题探究思考：将y=lgx放大1000倍，将函数y=1000lgx与比较，仍有上面规律吗？110yxxy21104220633084401055012660147701688018990211002321025320274302954031650337603587037980400904220044310464204853050640527502110422063308440105501266014770O仍然有随着x的增大，一次函数y=kx(k>0)保持固定的增长速度，而对数数的增长速度越来越慢.log1ayxa不论a值比k值大多少，在一定范围内，可能会大于kx，但由于的增长会慢于kx的增长，因此总存在一个x0，当x>x0时，恒有.logaxlogaxlogaxkx归纳总结三种函数模型的性质y＝ax(a>1)y＝logax(a>1)y＝nx(n>0)在(0，＋∞)上的增减性增函数增函数增函数图象的变化趋势随x增大逐渐近似与y轴——平行随x增大逐渐近似与x——轴平行增长速度不变增长速度①y＝ax(a>1)：随着x的增大，y增长速度越来越快，会远远大于y＝nx(n>0)的增长速度，y＝logax(a>1)的增长速度越来越慢②存在一个x0，当x>x0时，有ax>x——n>logx增函数增函数增函数y轴x轴越来越快越来越慢ax>nx>logax跟踪训练课本P139.2-4题1．下列函数中随x的增大而增大且速度最快的是()A．y＝exB．y＝lnxC．y＝x2D．y＝e－x当堂达标2．能使不等式log2x4时，log2x1)y＝logax(a>1)y＝nx(n>0)在(0，＋∞)上的增减性增函数增函数增函数图象的变化趋势随x增大逐渐近似与y轴——平行随x增大逐渐近似与x——轴平行增长速度不变增长速度①y＝ax(a>1)：随着x的增大，y增长速度越来越快，会远远大于y＝nx(n>0)的增长速度，y＝logax(a>1)的增长速度越来越慢②存在一个x0，当x>x0时，有ax>x——n>logx增函数增函数增函数y轴x轴越来越快越来越慢ax>nx>logax