二次函数图像与性质VIP免费

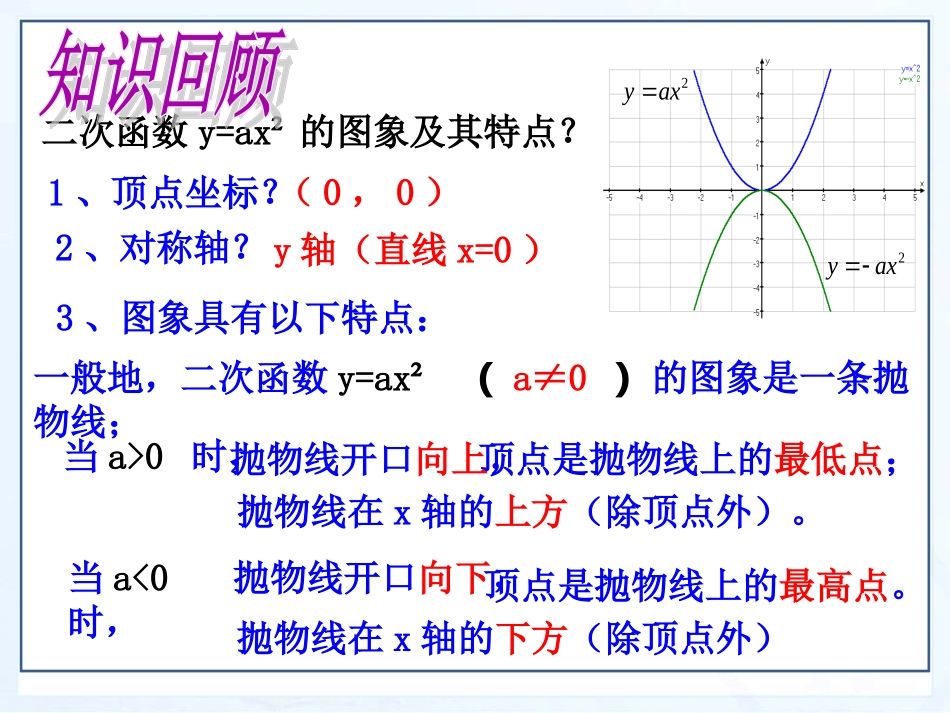
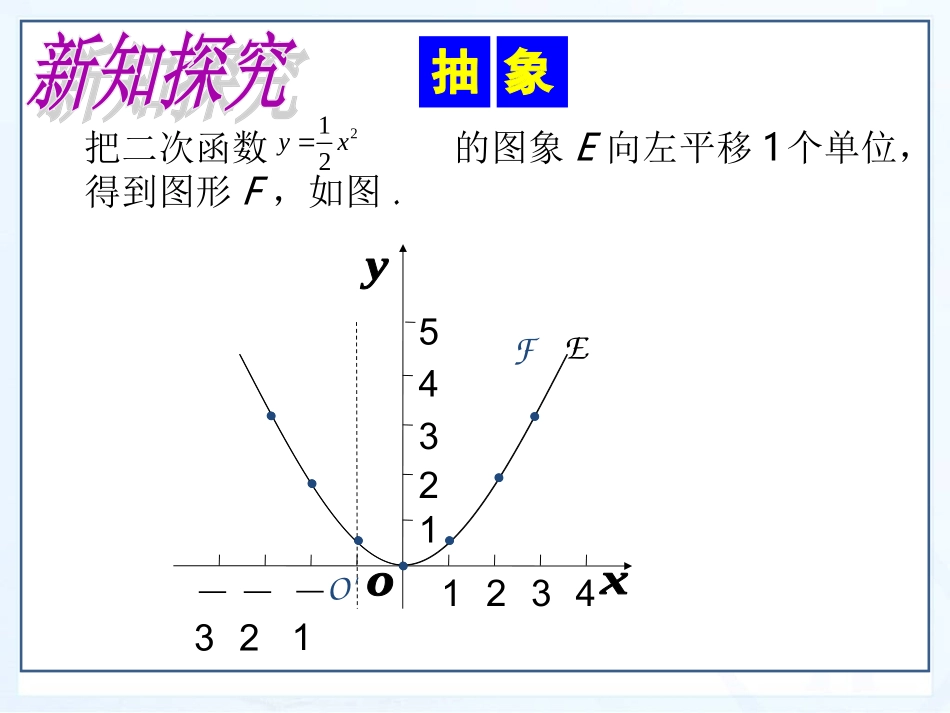
第一章二次函数二次函数y=ax²的图象及其特点？1、顶点坐标？（0，0）2、对称轴？y轴（直线x=0）3、图象具有以下特点：一般地，二次函数y=ax²（a≠0）的图象是一条抛物线；2yax2yax抛物线在x轴的下方（除顶点外）顶点是抛物线上的最高点。抛物线开口向下，当a<0时，抛物线在x轴的上方（除顶点外）。顶点是抛物线上的最低点；抛物线开口向上，当a>0时，把二次函数的图象E向左平移1个单位，得到图形F，如图.212yx123412345－1－2－3EFO'由于平移不改变图形的形状和大小，因此在向左平移1个单位后；原象象抛物线E:E的顶点O（0，0）E有对称轴l（与y轴重合）E开口向上212yx图形F也是抛物线点O'（－1，0）是F的顶点直线l`（过点O'与y轴平行）是F的对称轴F也开口向上在抛物线上任取一点，它在向左平移1个单位后，P的象点Q的坐标是什么？把点P的横坐标A减去1，纵坐标不变，即象点Q的坐标为212yx21(,)2paa212a21(1,)2aa抛物线F是哪个函数的图象呢？这样我们证明了：函数的图象是抛物线F，它的开口向上，它的顶点是O'（1，0），它的对称轴是过点O'（1，0）且平行与y轴的直线l'，直线l'是有横坐标为1的所有点组成的，我们把直线l'记做直线x=1，抛物线的开口向上.记从而点Q的坐标为这表明：点Q在函数的图象上，由此得出，抛物线F是函数的图象，证明：1,1baab则2121,bb21-x21y21-x21y21-x21y21-x21y类似地，我们可以证明下述结论：二次函数的图像是抛物线，它的对称轴是直线它的顶点坐标是（h，0）抛物线的开口向上；当a>0时抛物线开口向上；当时抛物线开口向下。0a由于我们已经知道了函数的图象的性质，因此今后在画的图象，只要先画出对称轴以及图象在对称轴右边的部分，然后利用对称性，画出左边的部分，在画图象的右边部分时，只需要“列表，描点，连线”三个步骤.2h-xayhx2h-xay2h-xay画函数的图象.2(2)yx解抛物线的对称轴是x=2，顶点坐标是（2，0）2(2)yx列表：自变量x从顶点的横坐标2开始取值.x22.534500.251492(2)yx描点和连线：画出图象在对称轴右边的部分.利用对称性画出图象在对称轴左边的部分:这样我们得到了函数的图象.2(2)yx1234－1－2－3－462841.说出下列二次函数的图象的对称轴和顶点坐标；21(1)(5)3yx2(2)3(2)yx对称轴x=5顶点坐标（5，0）对称轴x=-2顶点坐标（－2，0）2.画二次函数的图象2(1)yxx11.5233.50－0.25－1－4－6.252(1)yx－2－424－2－421x21y如何画二次函数的图象？我们来探究二次函数之间的关系.二次函数图象上的点横坐标纵坐标aa31-x21y231-x21y231-x21y231-a21221-x21y21-x21y21-a21通过上表说明与之间的关系？31-x21y221-x21y从此表看出：对于每个给定x值函数的值都要比函数都要大3由此可见函数的图象向上平移3个单位，就得到函数的图象.因此，二次函数的图象也是抛物线，它的对称轴为直线x=1（与抛物线的对称轴一样），顶点坐标为（1，3）（它是由抛物线的顶点（1，0）向上平移3个单位得到），它的开口向上.函数的图象是抛物线，它的对称轴是开口向上；当a＜0时，开口向下。.21-x21y31-x21y221-x21y21-x21y31-x21y231-x21y221-x21ykh-xay2直线x=h它的顶点坐标是(h,k)当a＞0时，抛物线的二次函数y=a(x-h)2+k的图象和性质１.顶点坐标与对称轴２.位置与开口方向３.增减性与最值抛物线顶点坐标对称轴位置开口方向增减性最值y=a(x-h)2+k(a>0)y=a(x-h)2+k(a<0)（h，k）（h，k）直线x=h直线x=h由h和k的符号确定由h和k的符号确定向上向下当x=h时,最小值为k.当x=h时,最大值为k.在对称轴的左侧,y随着x的增大而减小.在对称轴的右侧,y随着x的增大而增大.在对称轴的左侧,y随着x的增大而增大.在对称轴的右侧,y随着x的增大而减小.根据图形填表：第一步：写出对称轴和顶点坐标，并且在平面直角坐标系内画出对称轴，描出顶点；第三步：利用对称性，画出图象在对称轴左边的部分（这只要先把对称轴左边的对应点...