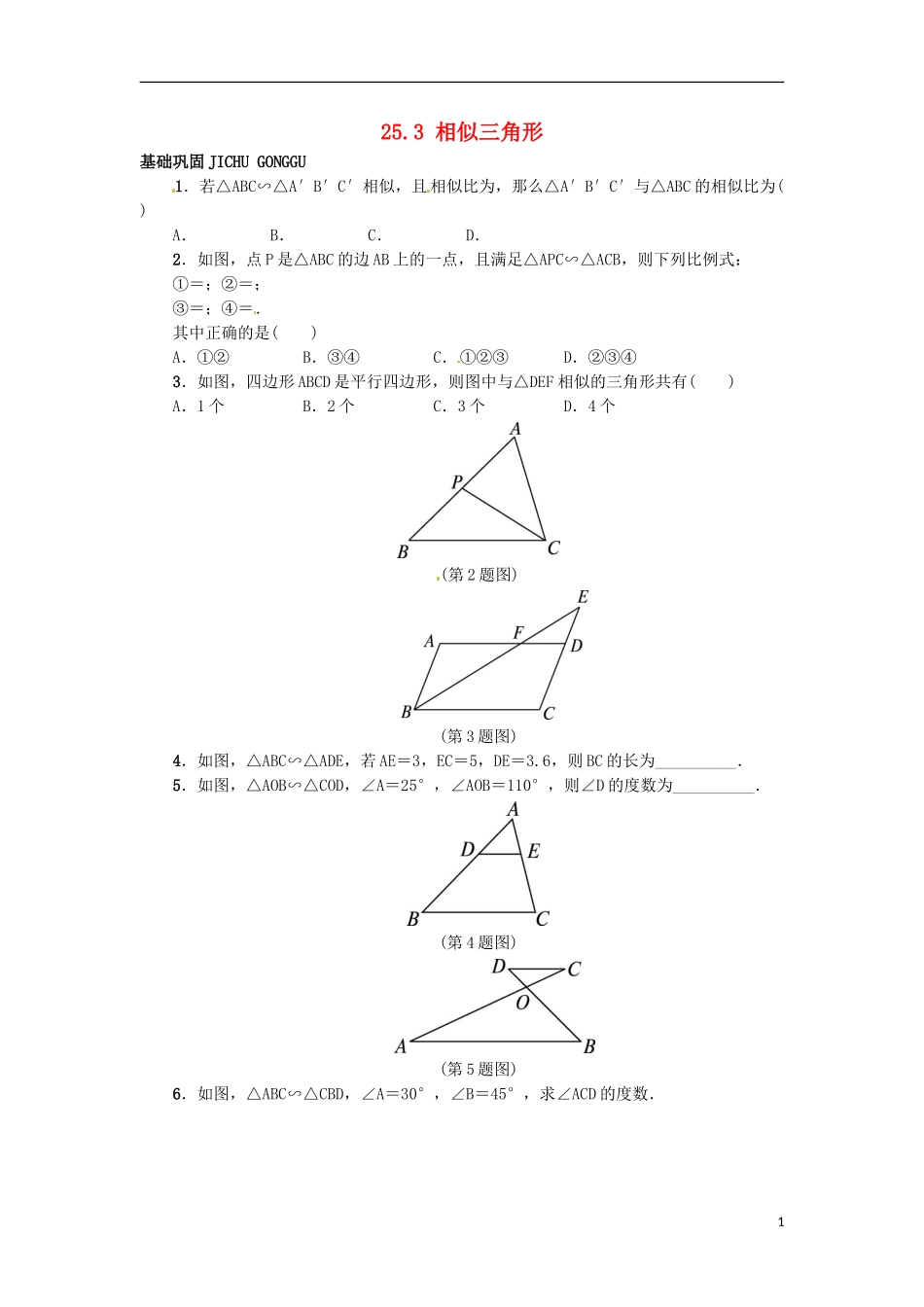
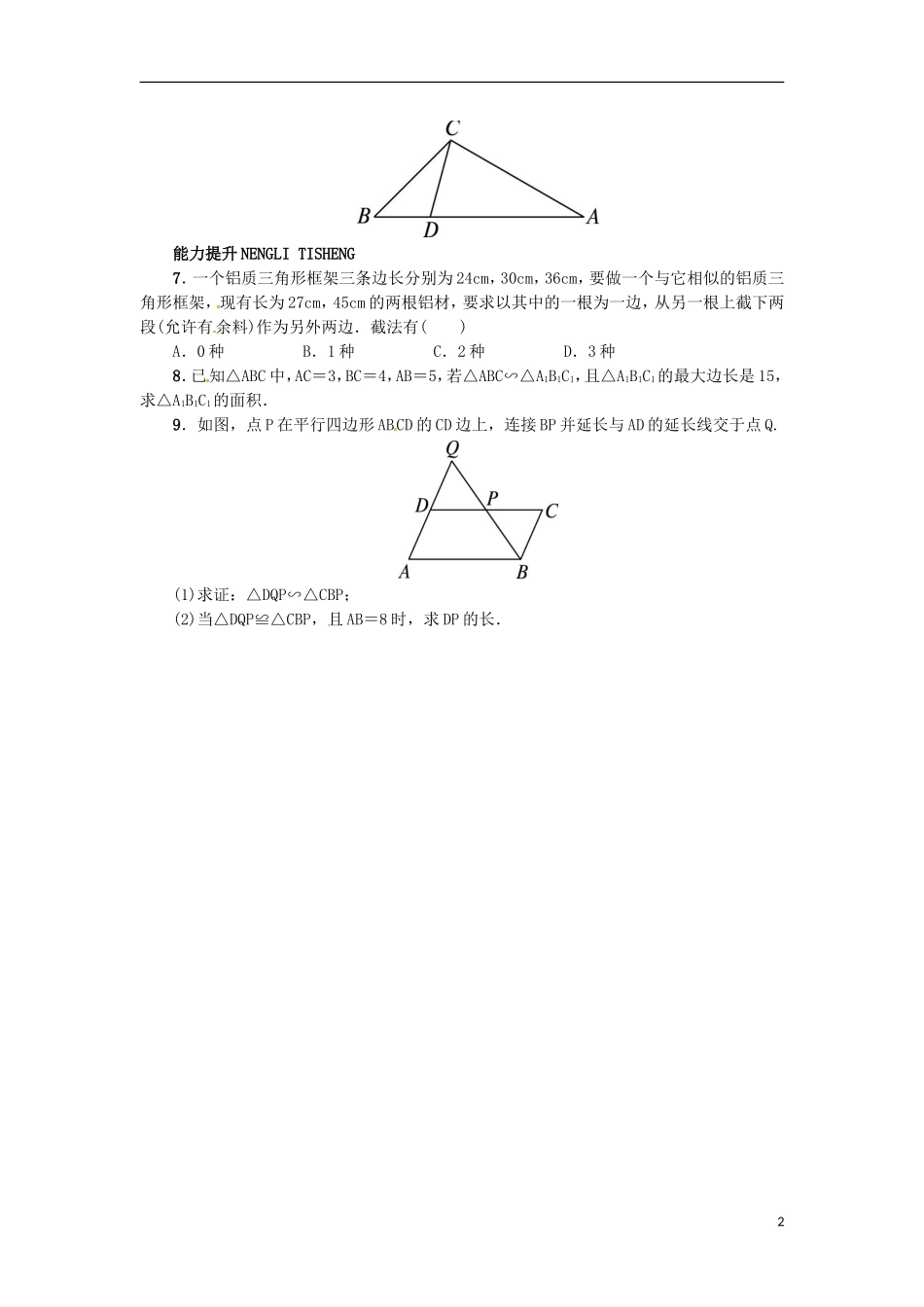
25.3相似三角形基础巩固JICHUGONGGU1.若△ABC∽△A′B′C′相似,且相似比为,那么△A′B′C′与△ABC的相似比为()A.B.C.D.2.如图,点P是△ABC的边AB上的一点,且满足△APC∽△ACB,则下列比例式:①=;②=;③=;④=.其中正确的是()A.①②B.③④C.①②③D.②③④3.如图,四边形ABCD是平行四边形,则图中与△DEF相似的三角形共有()A.1个B.2个C.3个D.4个(第2题图)(第3题图)4.如图,△ABC∽△ADE,若AE=3,EC=5,DE=3.6,则BC的长为__________.5.如图,△AOB∽△COD,∠A=25°,∠AOB=110°,则∠D的度数为__________.(第4题图)(第5题图)6.如图,△ABC∽△CBD,∠A=30°,∠B=45°,求∠ACD的度数.1能力提升NENGLITISHENG7.一个铝质三角形框架三条边长分别为24cm,30cm,36cm,要做一个与它相似的铝质三角形框架,现有长为27cm,45cm的两根铝材,要求以其中的一根为一边,从另一根上截下两段(允许有余料)作为另外两边.截法有()A.0种B.1种C.2种D.3种8.已知△ABC中,AC=3,BC=4,AB=5,若△ABC∽△A1B1C1,且△A1B1C1的最大边长是15,求△A1B1C1的面积.9.如图,点P在平行四边形ABCD的CD边上,连接BP并延长与AD的延长线交于点Q.(1)求证:△DQP∽△CBP;(2)当△DQP≌△CBP,且AB=8时,求DP的长.2参考答案1.B点拨:因为△ABC∽△A′B′C′相似,所以=,而△A′B′C′与△ABC的相似比为=.2.A点拨:根据相似三角形的对应边成比例判断比例式是否成立,由△APC∽△ACB得==,将比例式进行适当变形可知①,②是正确的;③,④是错误的.3.B点拨:由四边形ABCD是平行四边形,我们可以知道AD∥BC,所以△EDF∽△ECB.同时AB∥CD,故△DEF∽△ABF.综上所述,图中与△DEF相似的三角形共有2个.4.9.6点拨:由已知得AC=AE+EC=8,因为△ABC∽△ADE,所以=,即=,所以BC=9.6.5.45°点拨:由三角形内角和180°可知∠B=45°,因为△AOB∽△COD,所以∠D=∠B=45°.6.分析:在△ABC中,已知∠A和∠B,根据三角形内角和求出∠ACB的度数,由相似三角形对应角相等可以知道∠BCD的度数,利用∠ACB,∠BCD两角之差的关系计算∠ACD的度数即可.解:因为∠A=30°,∠B=45°,所以∠ACB=105°.因为△ABC∽△CBD,所以∠BCD=∠A=30°.所以∠ACD=∠ACB-∠BCD=105°-30°=75°.7.B点拨:分类讨论,假设以27cm为一边,把45cm截成两段,设这两段分别为xcm,ycm(x<y).则可得:==①或==②(注:27cm不可能是最小边),由①解得x=18,y=22.5,符合题意;由②解得x=,y=,x+y=+==54>45,不合题意,舍去;假设以45cm为一边,把27cm截成两段,设这两段分别为xcm,ycm(x<y).则可得:==(注:只能是45是最大边),解得x=30,y=,x+y=30+37.5=67.5>27,不合题意,舍去.8.分析:根据勾股定理的逆定理判断三角形的形状,再利用相似列比例式计算有关边长(直角边的长),最后计算三角形的面积.解:因为32+42=52,所以△ABC是直角三角形,且∠C=90°.因为△ABC∽△A1B1C1,所以△A1B1C1也是直角三角形,A1C1与B1C1垂直,A1B1=15,==,所以A1C1=·AC=9,B1C1=·BC=12.所以S△A1B1C1=A1C1·B1C1=×9×12=54.9.分析:(1)在平行四边形ABCD中,AD平行于BC,根据平行于三角形一边的直线和其他两边(或两边的延长线)相交,所截的三角形与原三角形相似,所以△DQP与△CBP相似;(2)△DQP≌△CBP,DP=CP=CD,AB=CD=8,即可得出答案.(1)证明:∵四边形ABCD是平行四边形,∴AQ∥BC,∴△DQP∽△CBP.(2)解:∵△DQP≌△CBP,3∴DP=CP=CD.∵AB=CD=8,∴DP=4.4