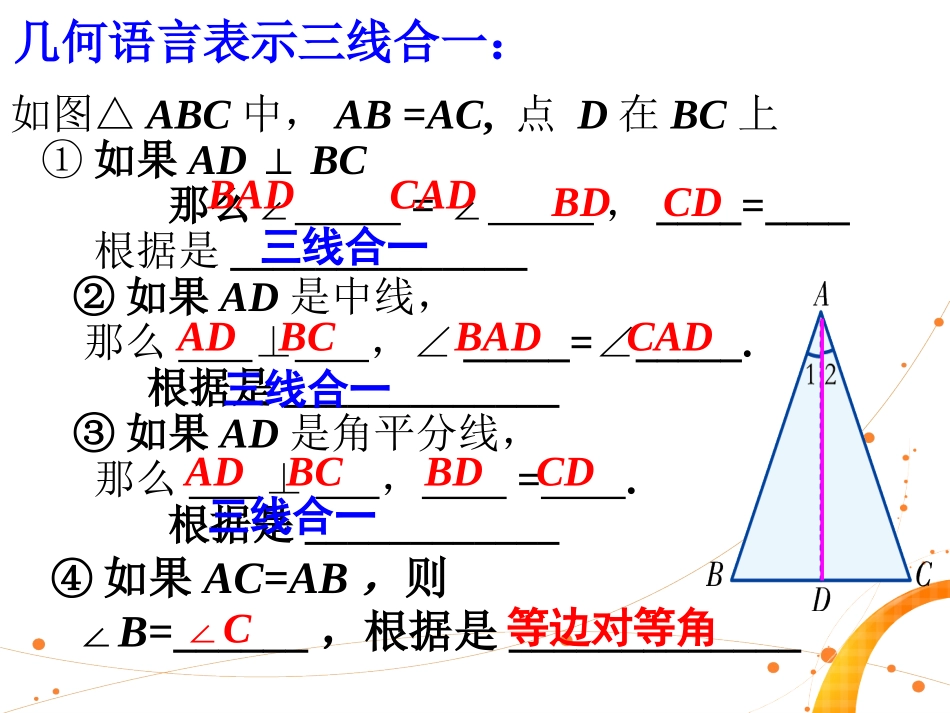
等腰三角形的性质有等腰三角形的性质有哪些?哪些?如图△ABC中,AB=AC,点D在BC上①如果AD⊥BC那么∠=∠,____=____根据是______________②如果AD是中线,那么⊥,∠_____=_____∠.根据是_____________③如果AD是角平分线,那么⊥,=.根据是____________BADCADBDCDBDCDBADCADADBCADBC几何语言表示三线合一:三线合一三线合一三线合一④如果AC=AB,则∠B=______,根据是_____________等边对等角∠C探究交流探究交流大家知道等腰三角形的两个底角相等,反过来它的逆命题是什么?1.猜想:如果一个三角形有两个角相等,那么这个三角形是等腰三角形.或:两个角相等的三角形是等腰三角形.猜想:这个命题正确吗?2.动手操作1.在纸上画一个线段BC。2.以BC为始边,分别以点B和点C为顶点,用量角器画两个相等的角,两角终边的交点为A。3.用刻度尺找出BC的中点D,连接AD,然后沿AD对折。问题1:AB与AC是否重合?说明了线段AB与线段AC有什么关系?问题2:本实验的条件与结论如何用文字语言加以叙述?有两个角相等的三角形是等腰三角形.等腰三角形的判定定理(简称“等角对等边”)在△ABC中∵∠B=C∠ABC几何语言:∴AB=AC(等角对等边)即△ABC是等腰三角形议一议:议一议:(1)“等角对等边”与“等边对等角”有何区别?①从边判断:等腰三角形的判定方法有:(等角对等边)判断一个三角形是等腰三角形有几种方法?②从角判断:有两边相等的三角形是等腰三角形.有两个角相等的三角形是等腰三角形.例1.在△ABC中,已知∠A=40°,∠B=70°,判断△ABC是什么三角形,为什么?例2.已知:如图,在△ABC中,AB=AC,点D,E分别是AB,AC上的点,且DE∥BC.求证:△ADE为等腰三角形.三个角都是60°的三角形是等边三角形吗?你能说明理由吗?由此得到一条等边三角形的判定定理:三个角都是60°的三角形是等边三角形三个角都是60°的三角形是等边三角形有一个角是60°的等腰三角形是等边三角形吗?为什么?动脑筋结论由此得到另一条等边三角形的判定定理:有一个角是60°的等腰三角形是等边三角形有一个角是60°的等腰三角形是等边三角形例3已知:如图,△ABC是等边三角形,点D,E分别在BA,CA的延长线上,且AD=AE.求证:△ADE是等边三角形.举例小结1、这节课我们学习了什么?2、等腰三角形的判定定理和性质定理有何联系?等腰三角形判定定理:如果一个三角形有两个角相等,那么这两个角所对的边也相等(等角对等边)。推论1:三个角相等的三角形是等边三角形。推论2:有一个角等于60°的等腰三角形是等边三角形