函数的奇偶性()VIP免费

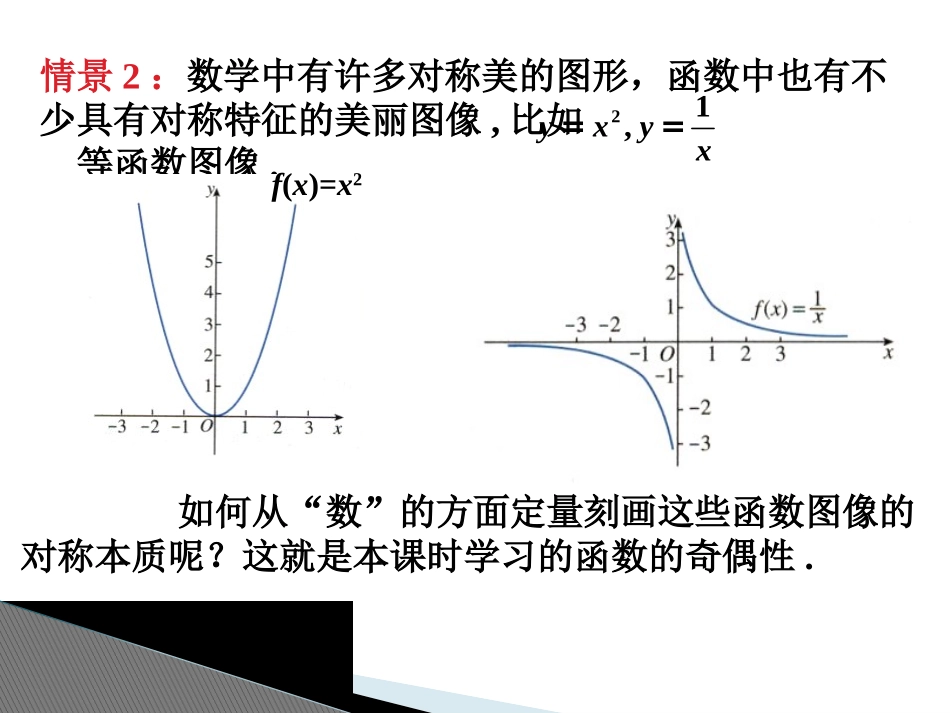
1.3.2奇偶性(1)情景1:观察下列图形,回顾轴对称与中心对称概念及其特征.情景导入情景2：数学中有许多对称美的图形，函数中也有不少具有对称特征的美丽图像,比如等函数图像.21,yxyx==f(x)=x2如何从“数”的方面定量刻画这些函数图像的对称本质呢？这就是本课时学习的函数的奇偶性.观察下图，思考并讨论以下问题：(1)这两个函数图象有什么共同特征吗？(2)如何利用函数解析式描述函数图象的这个特征呢？f(-3)=9=f(3)f(-2)=4=f(2)f(-1)=1=f(1)f(-3)=3=f(3)f(-2)=2=f(2)f(-1)=1=f(1)f(x)=x2f(x)=|x|实际上，对于R内任意的一个x,都有f(-x)=(-x)2=x2=f(x),这时我们称函数y=x2为偶函数.定义:一般地,对于函数f(x)的定义域内的任意一个x，都有f(－x)=f(x)，那么f(x)就叫做偶函数．观察函数f(x)=x和的图象(下图)，你能发现两个函数图象有什么共同特征吗？f(-3)=-3=-f(3)f(-2)=-2=-f(2)f(-1)=-1=-f(1)实际上，对于R内任意的一个x,都有f(-x)=-x=-f(x),这时我们称函数y=x为奇函数.f(-3)=-1/3=-f(3)f(-2)=-1/2=-f(2)f(-1)=-1=-f(1)1()fxx定义:一般地,对于函数f(x)的定义域内的任意一个x，都有f(－x)=－f(x)，那么f(x)就叫做奇函数．偶函数:一般地,对于函数f(x)的定义域内的任意一个x，都有f(－x)=f(x)，那么f(x)就叫做偶函数．奇函数:一般地,对于函数f(x)的定义域内的任意一个x，都有f(－x)=－f(x)，那么f(x)就叫做奇函数．定义注意：1、函数是奇函数或是偶函数称为函数的奇偶性.3、由定义可知，函数具有奇偶性的一个必要条件是，对于定义域内的任意一个x，则－x也一定是定义域内的（即定义域关于原点对称）．2、定义中“任意”二字，说明函数的奇偶性在定义域上的一个整体性质，它不同于函数的单调性.例1、判断下列函数的奇偶性：452(1)()(2)()11(3)()(4)()fxxfxxfxxfxxx(1)定义域为(-∞,+∞)即f(-x)=f(x)∴f(x)是偶函数.(2)定义域为(-∞,+∞)即f(-x)=-f(x)∴f(x)是奇函数.(3)定义域为{x|x≠0}(4)定义域为{x|x≠0}即f(-x)=-f(x)∴f(x)是奇函数.即f(-x)=f(x)∴f(x)是偶函数.解：∵f(-x)=(-x)4=f(x)∵f(-x)=(-x)5=-x5=-f(x)∵f(-x)=-x+1/(-x)=-f(x)∵f(-x)=1/(-x)2=f(x)(1)、先求定义域，看是否关于原点对称；(2)、再判断f(-x)=-f(x)或f(-x)=f(x)是否恒成立.用定义判断函数奇偶性的步骤：即f(-x)＋f(x)=0或f(-x)－f(x)=0是否恒成立.例2.判断下列函数的奇偶性：1(3)()(1)1xfxxx；(1)()|1||1|fxxx；(2)()0fx；解：(1)∵f(x)的定义域是R，且()|1||1|fxxx|1||1|xx()fx∴f(x)是偶函数.(2)∵函数的定义域是R，且f(x)=0，f(-x)=0.∴f(-x)=-f(x)，f(-x)=f(x).∴函数f(x)=0既是奇函数也是偶函数.(1)(0)4()(1)(0).xxxfxxxx（）101xx∴函数的定义域[-1，1)(3)(1)(1)0(1)xxx11x1(3)()(1)1xfxxx；解：关于原点不对称，∴函数f(x)既不是奇函数也不是偶函数.(1)(0)4()(1)(0).xxxfxxxx（）(4)∵f(x)的定义域是(－∞，0)∪(0，+∞)，当x＞0时，－x＜0，∴f(－x)=当x＜0时，－x＞0，∴f(－x)=故f(x)为奇函数.=－x(1+x)=－f(x)(x＞0).=－f(x)(x＜0)，(－x)[1－(－x)]=－x(1－x)(－x)[1＋(－x)]综上：f(－x)=－f(x)解：(1)(0)4()(1)(0).xxxfxxxx（）∵f(x)的定义域是(－∞，0)∪(0，+∞)，当x＞0时，－x＜0，∴f(－x)=当x＜0时，－x＞0，∴f(－x)=故f(x)为奇函数.=－x(1+x)=－f(x)(x＞0).=－f(x)(x＜0)，(－x)[1－(－x)]=－x(1－x)(－x)[1＋(－x)]综上：f(－x)=－f(x)法2：∵f(x)的定义域是(－∞，0)∪(0，+∞)，(1)(0)()(1)(0)xxxfxxxx且(1)(0)(1)(0)xxxxxx()fx故f(x)为奇函数.即f(－x)=－f(x)的值为奇函数，试求设函数axaxxxf))(1()(1a思考：课后作业P36、练习