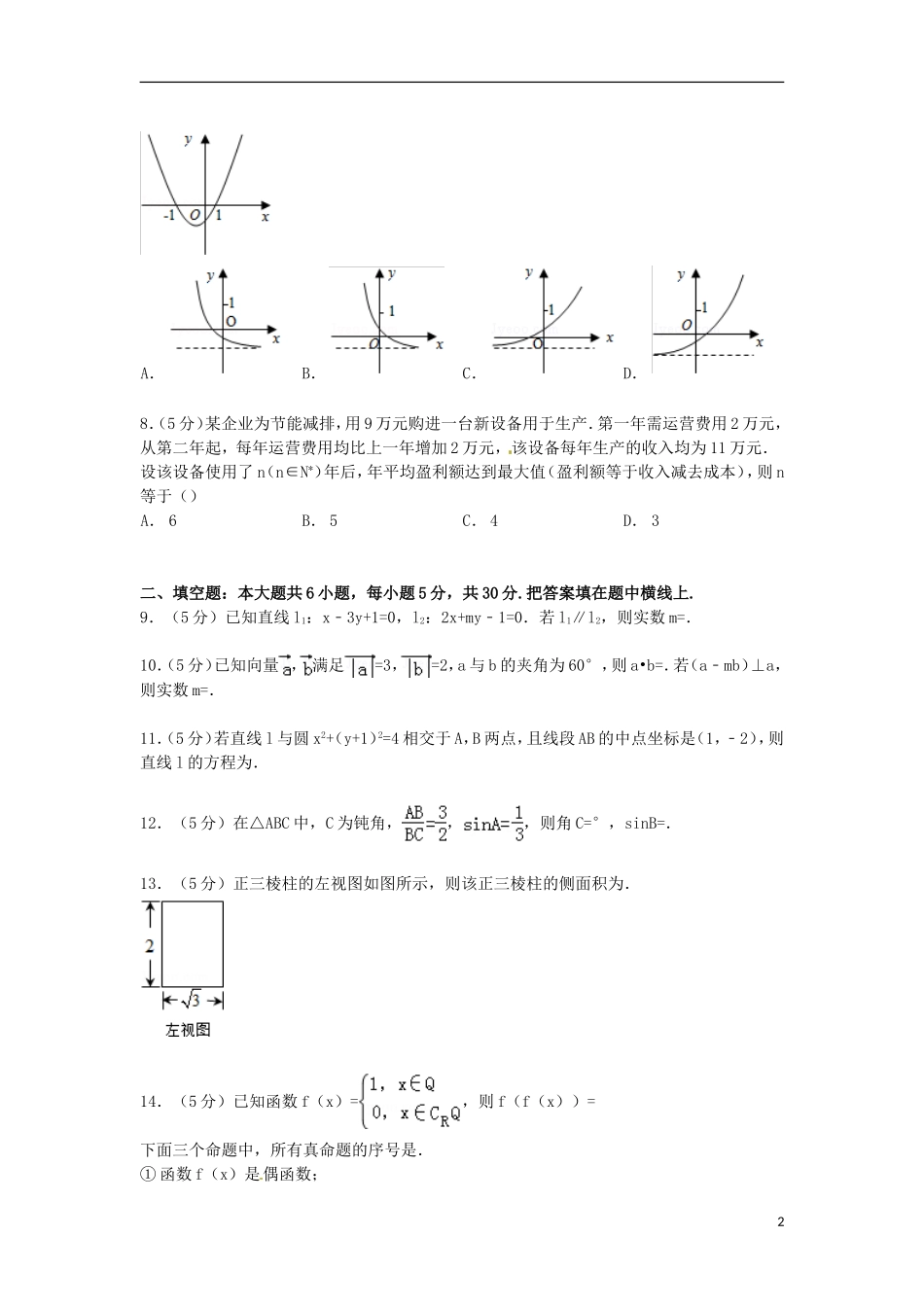
北京七中2015届高三上学期期中数学试卷(文科)一、选择题共8小题,每小题5分,共40分.在每小题列出的四个选项中,选出符合题目要求的一项.1.(5分)设全集U=R,集合A={x|x2﹣2x<0},B={x|x>1},则集合A∩∁UB=()A.{x|1<x<2}B.{x|1≤x<2}C.{x|0<x<1}D.{x|0<x≤1}2.(5分)设,则()A.c<b<aB.c<a<bC.a<b<cD.b<c<a3.(5分)设m、n是两条不同的直线,α,β,γ是三个不同的平面,给出下列四个命题:①若m⊥α,n∥α,则m⊥n②若m∥α,n∥α,则m∥n③若α⊥γ,β⊥γ,则α∥β④若α∥β,β∥γ,m⊥α,则m⊥γ其中正确命题的序号是()A.①和②B.②和③C.③和④D.①和④4.(5分)设等比数列{an}的公比为q,前n项和为Sn,且a1>0.若S2>2a3,则q的取值范围是()A.B.C.D.5.(5分)已知命题p:∀x∈R,sin(π﹣x)=sinx;命题q:α,β均是第一象限的角,且α>β,则sinα>sinβ.下列命题是真命题的是()A.p∧¬qB.¬p∧¬qC.¬p∧qD.p∧q6.(5分)在约束条件下,当3≤s≤5时,目标函数z=3x+2y的最大值的变化范围是()A.B.C.D.7.(5分)已知函数f(x)=(x+a)(x﹣b)(其中a>b>0)的图象如右图所示,则函数g(x)=ax﹣b的图象大致为()1A.B.C.D.8.(5分)某企业为节能减排,用9万元购进一台新设备用于生产.第一年需运营费用2万元,从第二年起,每年运营费用均比上一年增加2万元,该设备每年生产的收入均为11万元.设该设备使用了n(n∈N*)年后,年平均盈利额达到最大值(盈利额等于收入减去成本),则n等于()A.6B.5C.4D.3二、填空题:本大题共6小题,每小题5分,共30分.把答案填在题中横线上.9.(5分)已知直线l1:x﹣3y+1=0,l2:2x+my﹣1=0.若l1∥l2,则实数m=.10.(5分)已知向量,满足=3,=2,a与b的夹角为60°,则a•b=.若(a﹣mb)⊥a,则实数m=.11.(5分)若直线l与圆x2+(y+1)2=4相交于A,B两点,且线段AB的中点坐标是(1,﹣2),则直线l的方程为.12.(5分)在△ABC中,C为钝角,,,则角C=°,sinB=.13.(5分)正三棱柱的左视图如图所示,则该正三棱柱的侧面积为.14.(5分)已知函数f(x)=,则f(f(x))=下面三个命题中,所有真命题的序号是.①函数f(x)是偶函数;2②任取一个不为零的有理数T,f(x+T)=f(x)对x∈R恒成立;③存在三个点A(x1,f(x1)),B(x2,f(x2)),C(x3,f(x3)),使得△ABC为等边三角形.三、解答题共6小题,共80分.解答应写出文字说明,演算步骤或证明过程.15.(13分)△ABC的内角A,B,C的对边a,b,c满足b2+c2﹣a2=bc.(1)求角A的大小;(2)设函数f(x)=sincos+cos2,求f(B)的最大值.16.(13分)已知数列{an}是等差数列,a1=2,且a2,a4,a8成等比数列.(I)求等差数列{an}的通项公式;(II)如果数列{bn}是等比数列,且b1=a2,b2=a4,求{bn}的前n项和Sn.17.(13分)如图,正方形ADEF与梯形ABCD所在的平面互相垂直,AD⊥CD,AB∥CD,AB=AD=2,CD=4,M为CE的中点.(Ⅰ)求证:ED⊥BC;(Ⅱ)求证:平面BDE⊥平面BEC;(Ⅲ)判断直线BM和平面ADEF的位置关系,并加以证明.18.(13分)设a>0且a≠0,函数.(1)当a=2时,求曲线y=f(x)在(3,f(3))处切线的斜率;(2)求函数f(x)的极值点.19.(14分)已知椭圆C:+=1(a>b>0)的一个顶点为A(2,0),离心率为,直线y=k(x﹣1)与椭圆C交于不同的两点M,N,(Ⅰ)求椭圆C的方程;(Ⅱ)当△AMN的面积为时,求k的值.20.(14分)设正数数列{an}的前n项之和为Sn满足Sn=()2(Ⅰ)求a1,a2,a3,a4;3(Ⅱ)推测数列{an}的通项公式,并进行证明;(Ⅲ)设bn=,数列{bn}的前n项和为Tn,若Tn<对一切n∈N*成立,求最小正整数m.北京七中2015届高三上学期期中数学试卷(文科)参考答案与试题解析一、选择题共8小题,每小题5分,共40分.在每小题列出的四个选项中,选出符合题目要求的一项.1.(5分)设全集U=R,集合A={x|x2﹣2x<0},B={x|x>1},则集合A∩∁UB=()A.{x|1<x<2}B.{x|1≤x<2}C.{x|0<x<1}D.{x|0<x≤1}考点:交、并、补集的混合运算....