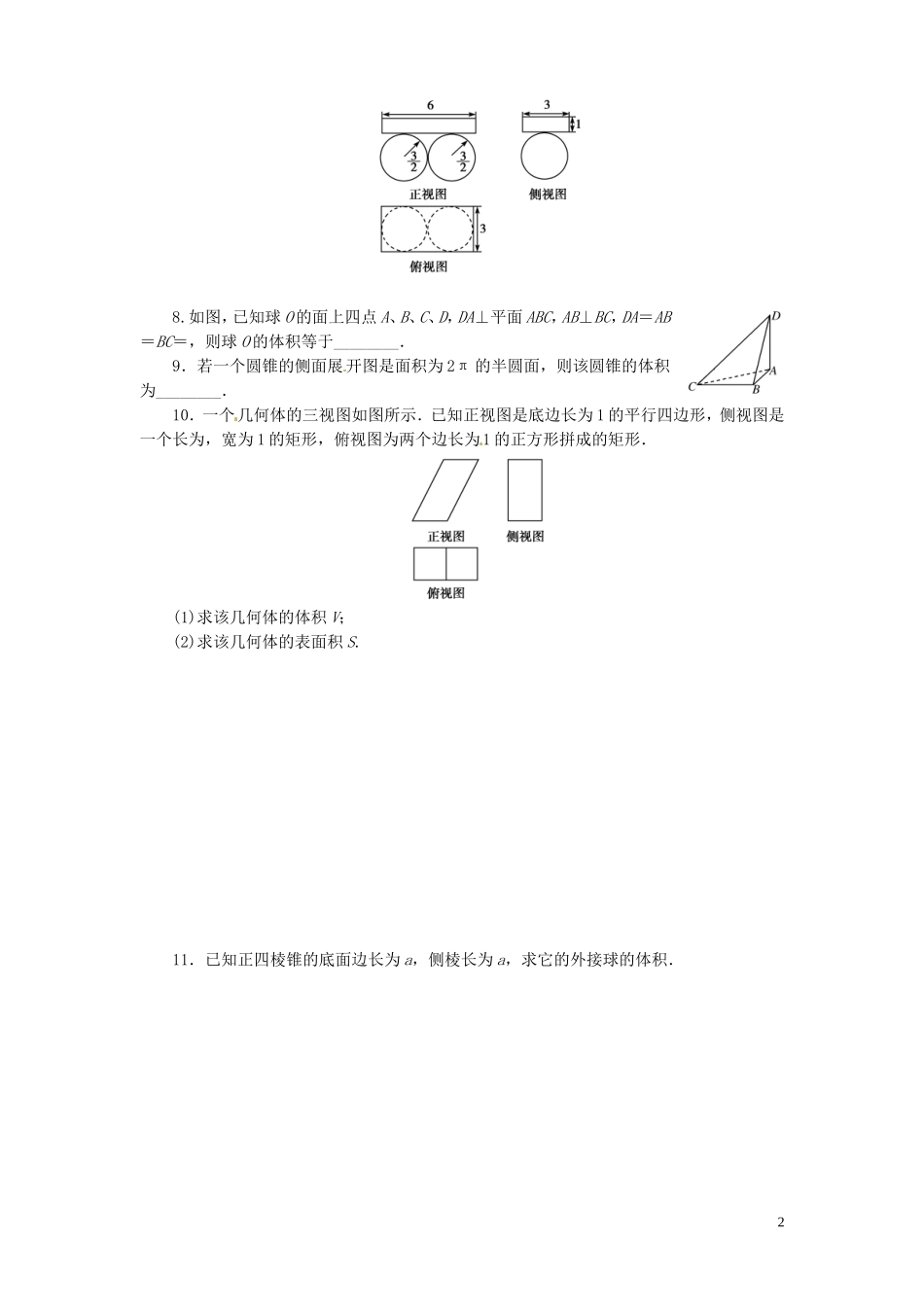
课时作业(四十)空间几何体的表面积和体积A级1.某四棱锥的三视图如图所示,该四棱锥的表面积是()A.32B.16+16C.48D.16+322.某几何体的三视图如图所示,它的体积为()A.12πB.45πC.57πD.81π3.过球的一条半径的中点作垂直于这条半径的球的截面,则此截面面积是球表面积的()A.B.C.D.4.圆台上、下底面面积分别是π、4π,侧面积是6π,这个圆台的体积是()A.πB.2πC.πD.π5.正六棱锥P-ABCDEF中,G为PB的中点,则三棱锥D-GAC与三棱锥P-GAC的体积之比为()A.1∶1B.1∶2C.2∶1D.3∶26.如图,正方体ABCD-A1B1C1D1的棱长为1,E,F分别为线段AA1,B1C上的点,则三棱锥D1-EDF的体积为________.7.一个几何体的三视图如图所示(单位:m),则该几何体的体积为________m3.18.如图,已知球O的面上四点A、B、C、D,DA⊥平面ABC,AB⊥BC,DA=AB=BC=,则球O的体积等于________.9.若一个圆锥的侧面展开图是面积为2π的半圆面,则该圆锥的体积为________.10.一个几何体的三视图如图所示.已知正视图是底边长为1的平行四边形,侧视图是一个长为,宽为1的矩形,俯视图为两个边长为1的正方形拼成的矩形.(1)求该几何体的体积V;(2)求该几何体的表面积S.11.已知正四棱锥的底面边长为a,侧棱长为a,求它的外接球的体积.2B级1.在矩形ABCD中,AB=4,BC=3,沿AC将矩形ABCD折成一个直二面角B-AC-D,则四面体ABCD的外接球的体积为()A.πB.πC.πD.π2.圆锥的全面积为15πcm2,侧面展开图的圆心角为60°,则该圆锥的体积为________cm3.3.如图所示,从三棱锥P-ABC的顶点P沿着三条侧棱PA,PB,PC剪开成平面图形得到△P1P2P3,且P2P1=P2P3.(1)在三棱锥P-ABC中,求证:PA⊥BC.(2)若P1P2=26,P1P3=20,求三棱锥P-ABC的体积.答案:课时作业(四十)A级1.B由三视图还原几何体的直观图如图所示.S表=×4+4×4=16+16.2.C由三视图知该几何体是由圆柱、圆锥两几何体组合而成,直观图如图所示.圆锥的底面半径为3,高为4,圆柱的底面半径为3,高为5,∴V=V圆锥+V圆柱=Sh1+Sh2=×π×32×4+π×32×5=57π.3.B由题意可得截面圆半径为R(R为球的半径),所以截面面积为π2=πR2,又球的表面积为4πR2,则=,故选B.4.D上底半径r=1,下底半径R=2. S侧=6π,设母线长为l,则π(1+2)·l=6π,∴l=2,∴高h==,∴V=π·×(12+1×2+22)=π.5.C G为PB中点,∴VP-GAC=VP-ABC-VG-ABC=2VG-ABC-VG-ABC=VG-ABC,又多边形ABCDEF是正六边形,∴S△ABC=S△ACD,∴VD-GAC=VG-ACD=2VG-ABC,∴VD-GAC∶VP-GAC=2∶1,故选C.36.解析:三棱锥D1-EDF的体积即为三棱锥F-DD1E的体积.因为E,F分别为AA1,B1C上的点,所以在正方体ABCD-A1B1C1D1中△EDD1的面积为定值,F到平面AA1D1D的距离为定值1,所以VF-DD1E=××1=.答案:7.解析:由三视图知,几何体下面是两个球,球半径为;上面是长方体,其长、宽、高分别为6、3、1,所以V=π××2+1×3×6=9π+18.答案:18+9π8.解析:如图所示,画出正方体,则2R=CD==,∴R=,V=πR3=π3=π.答案:π9.解析:设圆锥底面半径为r,母线长为l,高为h,则∴∴h=.∴V圆锥=π×12×=π.答案:π10.解析:(1)由三视图可知,该几何体是一个平行六面体(如图),其底面是边长为1的正方形,高为,所以V=1×1×=.(2)由三视图可知,该平行六面体中,A1D⊥平面ABCD,CD⊥平面BCC1B1,所以AA1=2,侧面ABB1A1,CDD1C1均为矩形.所以表面积S=2×(1×1+1×+1×2)=6+2.11.解析:如图所示,△SAC的外接圆是外接球的一个大圆,∴只要求出这个外接圆的半径即可,设外接球的半径为R,球心为O,则OA=OC=OS,∴O为△SAC的外心,即△SAC的外接圆半径就是球的半径. AB=BC=a,∴AC=a. SA=SC=AC=a,∴△SAC为正三角形.由正弦定理得2R===a,因此R=a,V球=πR3=πa3.B级1.C由题意知,球心到四个顶点的距离相等,所以球心在对角线AC上,且其半径为AC长度的一半,则V球=π×3=π.2.解析:设底面圆的半径为r,母线长为a,则侧面积为×(2πr)a=πra.由题意得,解得,故圆锥的高h==5,所...