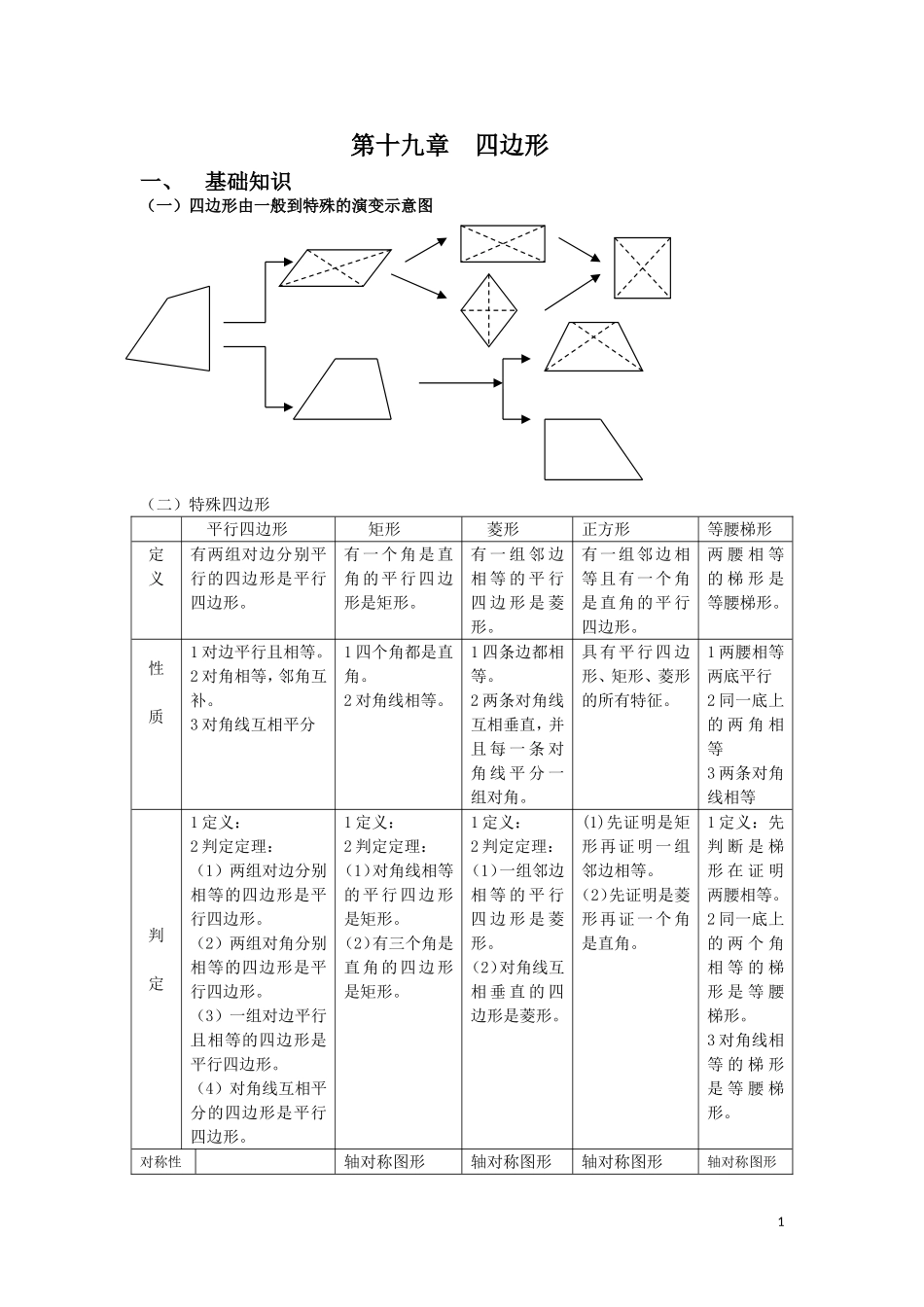
第十九章四边形一、基础知识(一)四边形由一般到特殊的演变示意图(二)特殊四边形平行四边形矩形菱形正方形等腰梯形定义有两组对边分别平行的四边形是平行四边形。有一个角是直角的平行四边形是矩形。有一组邻边相等的平行四边形是菱形。有一组邻边相等且有一个角是直角的平行四边形。两腰相等的梯形是等腰梯形。性质1对边平行且相等。2对角相等,邻角互补。3对角线互相平分1四个角都是直角。2对角线相等。1四条边都相等。2两条对角线互相垂直,并且每一条对角线平分一组对角。具有平行四边形、矩形、菱形的所有特征。1两腰相等两底平行2同一底上的两角相等3两条对角线相等判定1定义:2判定定理:(1)两组对边分别相等的四边形是平行四边形。(2)两组对角分别相等的四边形是平行四边形。(3)一组对边平行且相等的四边形是平行四边形。(4)对角线互相平分的四边形是平行四边形。1定义:2判定定理:(1)对角线相等的平行四边形是矩形。(2)有三个角是直角的四边形是矩形。1定义:2判定定理:(1)一组邻边相等的平行四边形是菱形。(2)对角线互相垂直的四边形是菱形。(1)先证明是矩形再证明一组邻边相等。(2)先证明是菱形再证一个角是直角。1定义:先判断是梯形在证明两腰相等。2同一底上的两个角相等的梯形是等腰梯形。3对角线相等的梯形是等腰梯形。对称性轴对称图形轴对称图形轴对称图形轴对称图形1(三)1.三角形中位线定理:三角形的中位线平行于三角形的第三边,且等于第三遍的一半。2.由矩形的性质得到直角三角形的一个性质:直角三角形斜边上的中线等于斜边的一半。二、例题例1:已知:如图,菱形ABCD中∠B=60°;E,F在边BC,CD上,且∠EAF=60°;求证:AE=AF.同类练习:如图,已知菱形ABCD中,∠B=∠EAF=60°,∠BAE=20°,求∠CEF.例2:如图,在的纸片中,AC⊥AB,AC与BD交于O,将△ABC沿对角线AC翻折得到.(1)求证:以A、C、D、为顶点的四边形是矩形;(2)若,求翻折后纸片重叠部分的面积,即.例4、已知:分别以的各边为边,在边的同侧作等边三角形、等边三角形和等边三角形,连结。(1)试说明四边形为平行四边形;(2)当满足什么条件时,四边形为菱形、矩形、正方形;EDFABC同类练习:中,,都是等边三角形。2FEDCBA求四边形的面积。DFEABC三、适时训练(一)精心选一选1.下列命题正确的是()一组对边相等,另一组对边平行的四边形一定是平行四边形对角线相等的四边形一定是矩形两条对角线互相垂直的四边形一定是菱形两条对角线相等且互相垂直平分的四边形一定是正方形2.已知平行四边形ABCD的周长32,5AB=3BC,则AC的取值范围为()A.6