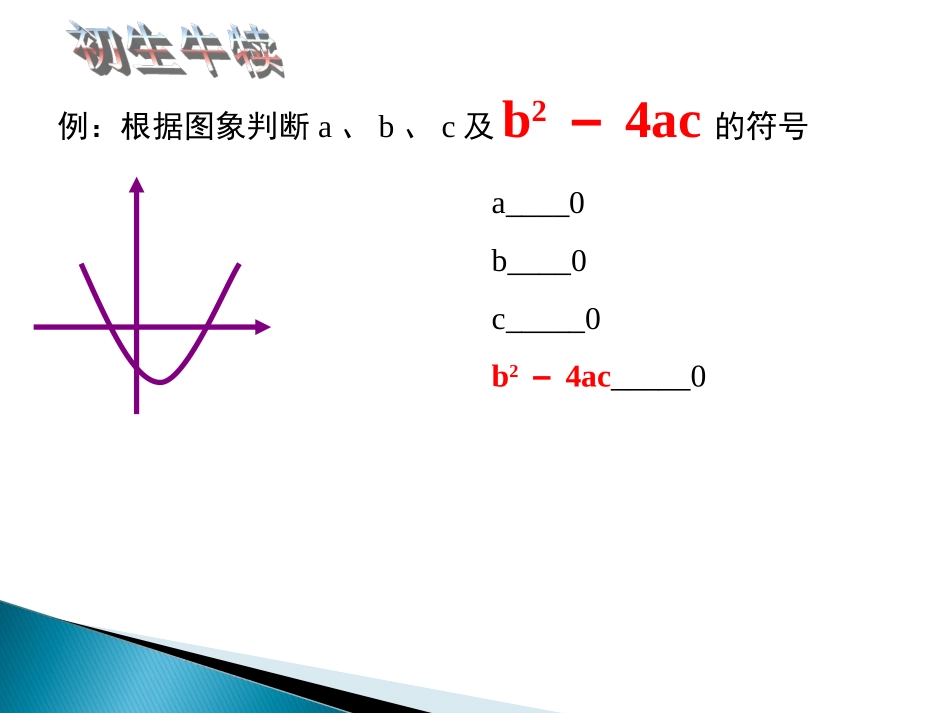
海亮初中宣淑嫒例:根据图象判断a、b、c及b2-4ac的符号a____0b____0c_____0b2-4ac_____01.a的符号当a>0时,抛物线开口向上;当a<0时,抛物线开口向下。|a|越大,抛物线的开口越窄;|a|相同,抛物线的开口大小相同知识链接抛物线开口向上抛物线开口向下a>0a<02.b的符号由于对称轴是x=-b/2a;a,b共同决定对称轴的位置.x=x=左同右异对称轴在y轴左侧>0a、b同号对称轴在y轴右侧<0;a、b异号2ba-2ba-2ba-2ba-3.c的符号决定抛物线与y轴交点的位置,交点坐标为(0,c)C>0交点在y轴正半轴C=0抛物线过原点C<0交点在y轴负半轴4.b2-4ac的符号抛物线与x轴的交点纵坐标为0,所以由y=ax2+bx+c(a≠0)得0=ax2+bx+c(a≠0),方程解的个数显示抛物线与x轴交点的个数。b2-4ac>0b2-4ac=0b2-4ac<0抛物线与x轴有两个交点抛物线与x轴有一个交点抛物线与x轴无交点例:根据图象判断a、b、c及b2-4ac的符号a____0b____0c_____0b2-4ac_____0><><根据图象判断a、b、c及b2-4ac的符号a____0b____0c_____0b2-4ac_____0a____0b____0c_____0b2-4ac_____0>>=><><<在二次函数y=ax2+bx+c(a≠0)的图象中,a、b、c皆为正数,则其图像永远不经过()。A、第一象限B、第二象限C、第三象限D、第四象限D例:已知二次函数的图像如图所示,下列结论:⑴a+b+c﹤0⑵a-b+c﹥0⑶abc﹥0⑷b=2a其中正确的结论的个数是()A1个B2个C3个D4个Dx-110y卧冰求鲤归纳:由x=1时抛物线上的点的位置确定。(2)a-b+c的符号:由x=-1时抛物线上的点的位置确定(3)b与2a之间的关系:由对称轴直线X=位置确定。(1)a+b+c的符号2ba-二次函数y=ax2+bx+c(a≠0)的图象如图所示,下列判断不正确的是()A、abc>0,B、b2-4ac<0,C、a-b+c<0,D、4a+2b+c>0.xyo-12D卧冰求鲤1.如果函数y=kx+b的图象在第一、二、三象限内,那么函数y=kx2+bx-1的图象大致是()1A-1B1C-1DB2.二次函数y=ax2+bx+c(a≠0)与一次函数y=ax+c在同一坐标系内的大致图象是()xyoxyoxyoxyo(C)(D)(B)(A)C(2015·咸宁)如图是二次函数y=ax²+bx+c的图象,下列结论:①二次三项式ax²+bx+c的最大值是4;②4a+2b+c<0;③一元二次方程ax²+bx+c=1的两根之和为-1;④使y≤3成立的x的取值范围是x≥0.其中正确的个数为()A.1B.2C.3D.4训练眼力:从图像你能得到哪些信息?新知链接►知识点二次函数的图象二次函数y=ax²+bx+c的图象(1)a<0开口向下,函数有最大值;a>0开口向上,函数只有最小值(2)二次函数图象与系数之间的关系(对称轴,特殊点)(3)二次函数与方程和不等式(组)的关系(2015·咸宁)如图是二次函数y=ax²+bx+c的图象,下列结论:①二次三项式ax²+bx+c的最大值是4;∵开口向下a<0又∵顶点坐标(-1,4)∴二次函数y=ax²+bx+c最大值为4即二次三项式ax²+bx+c的最大值是4,故①正确②4a+2b+c<0;由图像知:当x=2时,y<0∴4a+2b+c<0,故②正确2③一元二次方程ax²+bx+c=1的两根之和为-1;y=1x=-1根据抛物线的对称性可知,一元二次方程ax²+bx+c=1的两根满足∴两根之和为-2,故③错误1212xx+=-④使y≤3成立的x的取值范围是x≥0.其中正确的个数为()A.1B.2C.3D.4y=3由图像知:使y≤3成立的x的取值范围是x≤-2或x≥0故④错误。所以这题选择B【方法总结】这种类型的题目主要考查形式为选择题,解决此类题型常用的方法是从二次函数的图象性质出发,通常把已知点坐标代入解析式中找出a,b,c的关系,再结合对称轴直线x=,确定a、b之间的等量关系,从而构造一些新的关系式。判断图像与x轴交点情况则利用判别式b²-4ac。2ba-如图是二次函数y=ax2+bx+c图象的一部分,图象过点A(X1,0),-3<X1<-2,对称轴为x=-1.给出四个结论:①abc>0;②2a+b=0;③b2>4ac;④a-b>m(ma+b)(m≠-1的实数);⑤3b+2c>0.其中正确的结论有()A.2个B.3个C.4个D.5个