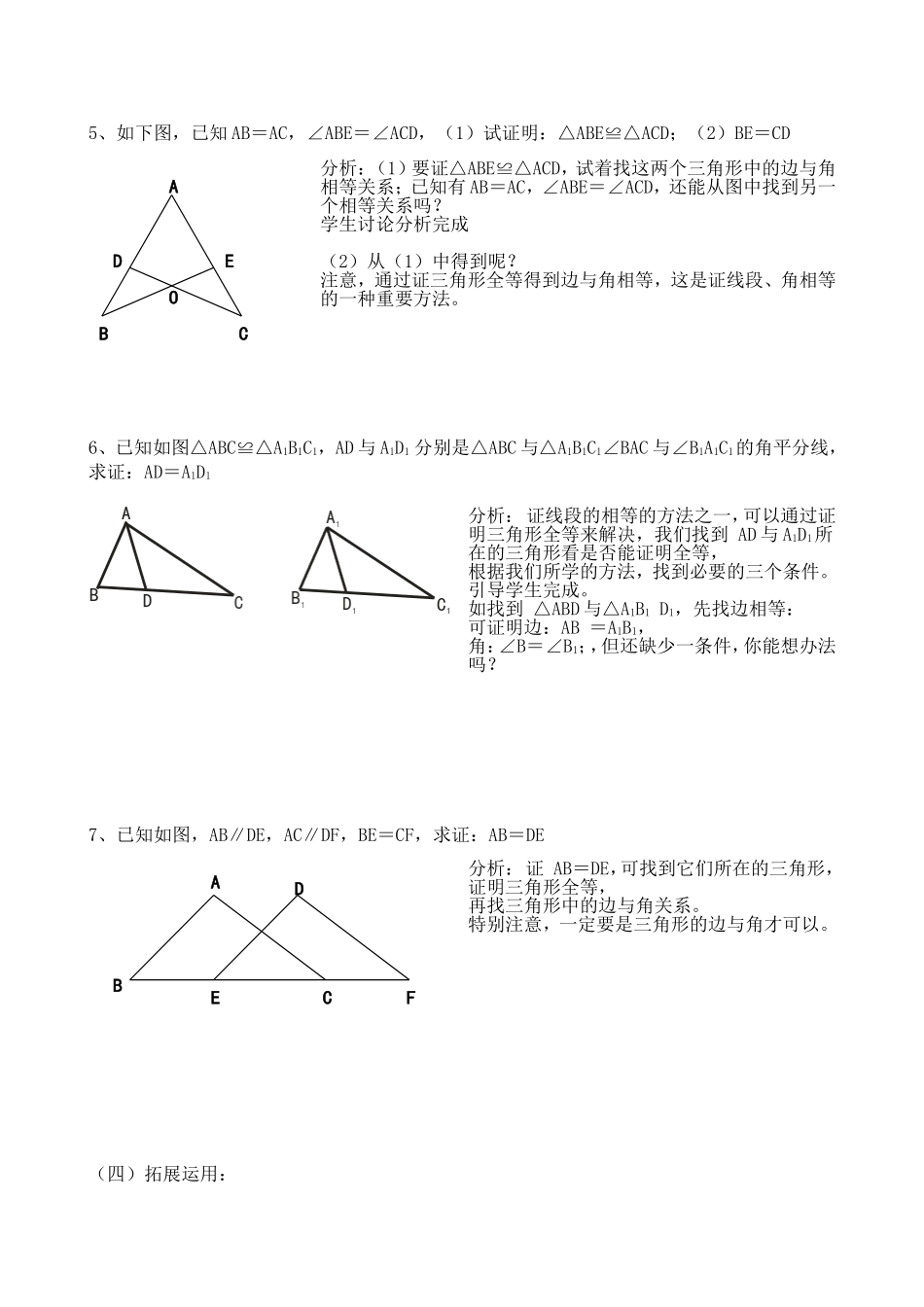
3.4.2三角形全等的判定2(ASA定理)教学目标知识技能1、掌握好ASA定理的内容及它的三个条件;2、能通过已知及推证得到必要的三个条件,从而证明两三角形全等;3、学会读图及通过已知进行推理。过程方法练习、讨论、交流、总结,从而熟练掌握好ASA定理及其运用情感态度价值观不断提高自身的分析问题解决问题的能力,并培养好严谨的治学态度。重点难点重点ASA定理的内容难点ASA定理的运用(一)、自学导读:1、判定两个三角形全等我们学过了什么方法?它有几个条件,其中有组角的关系,有组边的关系,它们之间有什么限制。2、如下图,试填空:(1)、在△ABC与△DEF中:∵AB=DEEF=BC∴△ABC≌△DEF(SAS)(2)、在△ABC与△DEF中∵=∠ACB=∠DFE=∴△ABC≌△DEF(SAS)回顾三角形全等判定定理SAS的运用的三个条件,及它们之间的限制关系。3、除了SAS判定定理外还有其他方法吗?可不可以将边与角互换呢?(二)、阅读教材P76页4、角边角定理的内容。类比边角边定理。定理的理解:如下图定理有三个条件,其中有组边的关系,有组角关系,边一定是两组角的夹边。(三)定理的运用:BCEF(1)、在△ABC与△DEF中:∵=AB=DE=∴△ABC≌△DEF(ASA)(2)、在△ABC与△DEF中∵∠ACB=∠DFE=∠ABC=∠DEF∴△ABC≌△DEF(ASA)BCEFADAD5、如下图,已知AB=AC,∠ABE=∠ACD,(1)试证明:△ABE≌△ACD;(2)BE=CD6、已知如图△ABC≌△A1B1C1,AD与A1D1分别是△ABC与△A1B1C1∠BAC与∠B1A1C1的角平分线,求证:AD=A1D17、已知如图,AB∥DE,AC∥DF,BE=CF,求证:AB=DE(四)拓展运用:分析:(1)要证△ABE≌△ACD,试着找这两个三角形中的边与角相等关系;已知有AB=AC,∠ABE=∠ACD,还能从图中找到另一个相等关系吗?学生讨论分析完成(2)从(1)中得到呢?注意,通过证三角形全等得到边与角相等,这是证线段、角相等的一种重要方法。BCODEA分析:证线段的相等的方法之一,可以通过证明三角形全等来解决,我们找到AD与A1D1所在的三角形看是否能证明全等,根据我们所学的方法,找到必要的三个条件。引导学生完成。如找到△ABD与△A1B1D1,先找边相等:可证明边:AB=A1B1,角:∠B=∠B1;,但还缺少一条件,你能想办法吗?分析:证AB=DE,可找到它们所在的三角形,证明三角形全等,再找三角形中的边与角关系。特别注意,一定要是三角形的边与角才可以。ABECFD(五)小结:1、我们学习了两个判定三角形全等的方法,分别是与。它们都必需满足三个条件,我们要记牢。2、证明线段及角相等的办法,可以通过证明它们所在的三角形全等来解决。(六)作业:基础训练:P36页:问题探究。8、已知如左图,△ABC中,BD=BE,∠BEC=∠BDA,AD与CE相交于点F,(1)试证明:AB=AC;(2)试判断△AFC的形状,并说明理由。(1)引导学生分析:证AB=AC的方法,再找到条件进行推理。(2)由第(1)的结论可以得到什么,再进行分析。CBFDEA