平面向量数乘运算及其几何意义VIP免费

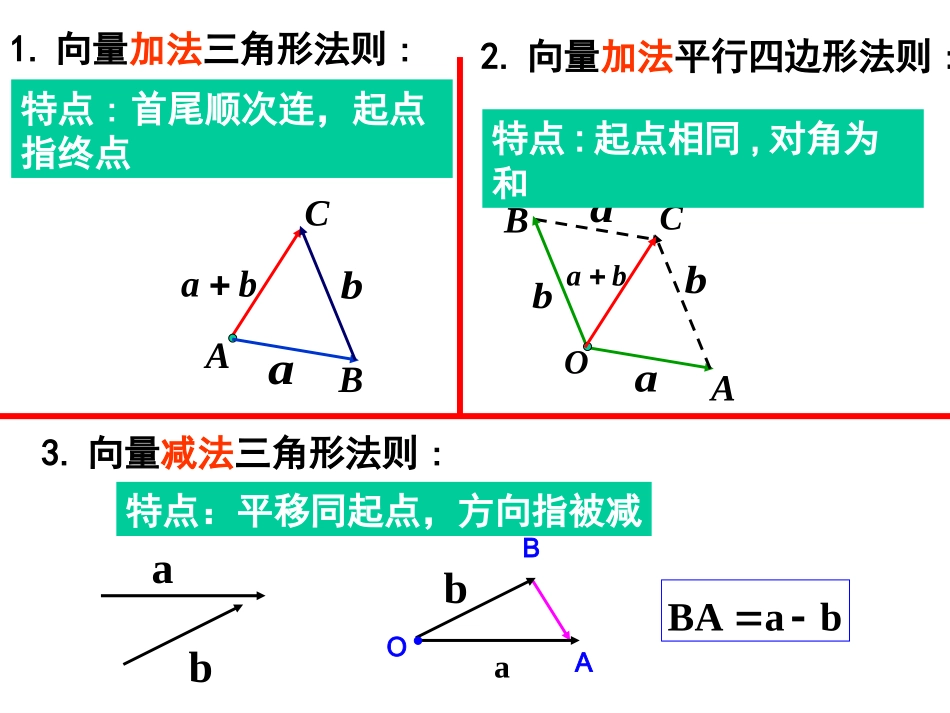
2.2.3向量数乘运算及其几何意义1.向量加法三角形法则:aAbBCbaaaAbBbOCba特点:首尾顺次连，起点指终点特点:起点相同,对角为和babBaABAab�O特点：平移同起点，方向指被减2.向量加法平行四边形法则:3.向量减法三角形法则:已知非零向量,作出,你能发现什么？aaaa类比上述结论，又如何呢？()()()aaaaOaaaABC3aPQaMaNa3a与方向相同3aa33aa即与方向相反3aa33aa即作一作，看成果一般地，我们规定实数λ与向量的积是一个向量，这种运算叫做向量的数乘，记作，它的长度和方向规定如下：aa||||||;aa（1）（2）当时，的方向与的方向相同；当时，的方向与的方向相反。aa0aa0特别的，当时，00.a书本P90,练习2,3练一练:(1)(1)根据定义，求作向量根据定义，求作向量3(23(2aa))和和(6(6aa))((aa为非零向量为非零向量))，并进行比较。，并进行比较。a)2(3a)2(3aa6=baba22a2b2baba22)(2(2)(2)已知向量已知向量a,ba,b，求作向量，求作向量2(2(a+ba+b))和和22a+a+22bb，并进行比较。，并进行比较。ab向量的数乘运算满足如下运算律：向量的数乘运算满足如下运算律：)();()1(2)(3);().aaaaaabab，是实数，）（（aaabab特别地:（）向量的加、减、数乘运算统称为向量的线性运算例1、计算下列各式a4)3)(1(ababa)(2)(3)2(a12b5)23()32)(3(cbacbacba25书本P90,练习5练一练::思考?,),0()1(位置关系如何则若baaab?),0(//)2(是否成立则若abaab//ba成立向量共线定理：0.),(,ababa向量与共线当且仅唯一一个当有实数使书本P90,练习4练一练:思考思考:1):1)为什么要是非零向量为什么要是非零向量??a2)2)可以是零向量吗可以是零向量吗??bab即与共线ba(0)a例例22如图，已知如图，已知AD=3ABAD=3AB，，DE=3BDE=3BCC，，试判断试判断ACAC与与AEAE是否共线。是否共线。ADECBBCAB33BCAB3AC3∴与共线．AEACDEADAE解：例3.如图，已知任意两个向量，试作ab、2,3.OBabOCab�,OAab�你能判断A、B、C三点之间的位置关系吗？为什么？abab2b3bABCO证明证明三点共线三点共线的方法的方法::总结:AB=λBCAB=λBC且有公共点Ｂ且有公共点ＢA,B,CA,B,C三点共线三点共线121212122362348:eeABeeBCeeCDeeAB��已知两个非零向量和不共线，如果，，，求证、、D三点共线.设是两个不共线的向量，，若A、B、D三点共线，求k的值.12122,3,ABekeCBee�12,ee�122CDee�例5.如图，平行四边形ABCD的两条对角线相交于点M，且，你能用、来表示。,ABaADb�abMAMBMCMD�、、和ABDCMab书本P92,11题练一练:CD④①②一、一、①①λλaa的定义及运算律的定义及运算律②②向量共线定理向量共线定理(a≠0)(a≠0)b=b=λλaa向量向量aa与与bb共线共线二、定理的应用：二、定理的应用：1.1.证明证明向量共线向量共线2.2.证明证明三点共线三点共线:AB=:AB=λλBCBC且有公共点且有公共点ＢＢ3.3.证明证明两直线平行两直线平行::AB=AB=λλCDCDABAB与与CDCD不在同一直线上不在同一直线上直线直线AB∥AB∥直线直线CDCD小结:A,B,CA,B,C三点共线三点共线ABCD∥ABCD∥书本P91，A组，9,10B组,3