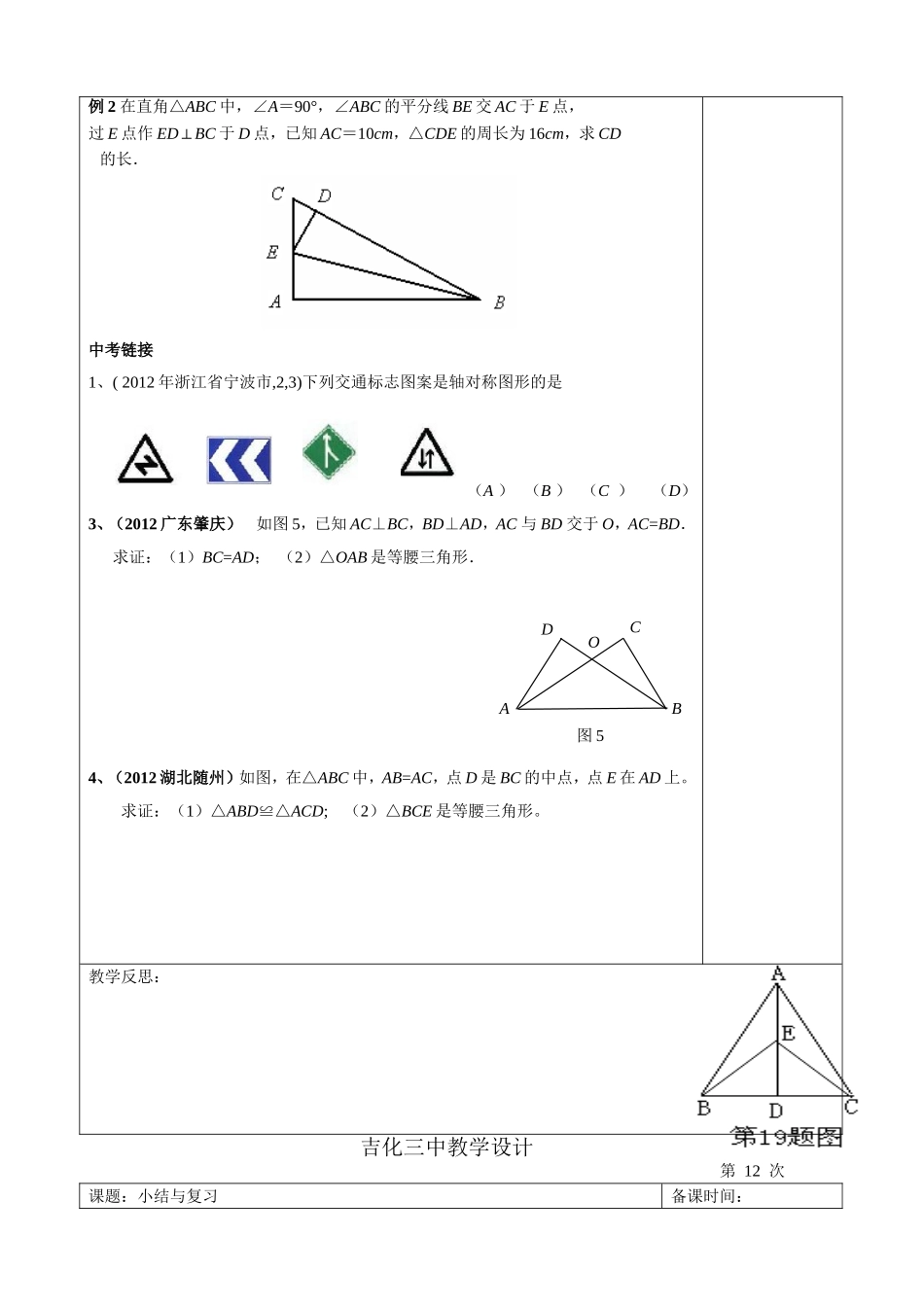
吉化三中教学设计第11次课题:小结与复习课型:新课备课时间:授课时间:教学目标:知识技能过程与方法德育渗透体会轴对称的思想,同时由特殊到一般的思想、分类讨论的思想、数形结合的思想及方程的思想都应引起广泛的重视和应用.教学重点:轴对称、轴对称变换、等腰三角形的性质和判定教学难点:等腰三角形的性质和判定.掌握等腰三角形的性质和判定,并能应用这些知识是学好本章的关键.例1已知△ABC是等边三角形,D是AC的中点,E是BC延长线上的一点,且CE=21BC,你能找出图中所有的等腰三角形吗?并说明理由?解(1)结论:△CED是等腰三角形.理由:因为△ABC是等边三角形,D是AC的中点.所以CD=21AC=21BC因为CE=21BC所以CD=CE所以△CED是等腰三角形.(2)结论:△BDE是等腰三角形.因为△CDE是等腰三角形且∠ACB=60°所以∠E=∠CDE=30°因为BD是等边三角形的中线,根据三线合一可得∠DBC=21∠ABC=30°所以∠E=∠DBC=30°,所以△BDE是等腰三角形.二次备课例2在直角△ABC中,∠A=90°,∠ABC的平分线BE交AC于E点,过E点作ED⊥BC于D点,已知AC=10cm,△CDE的周长为16cm,求CD的长.中考链接1、(2012年浙江省宁波市,2,3)下列交通标志图案是轴对称图形的是(A)(B)(C)(D)3、(2012广东肇庆)如图5,已知AC⊥BC,BD⊥AD,AC与BD交于O,AC=BD.求证:(1)BC=AD;(2)△OAB是等腰三角形.4、(2012湖北随州)如图,在△ABC中,AB=AC,点D是BC的中点,点E在AD上。求证:(1)△ABD≌△ACD;(2)△BCE是等腰三角形。教学反思:吉化三中教学设计第12次课题:小结与复习备课时间:ABCDO图5课型:新课授课时间:教学目标:知识技能过程与方法德育渗透体会轴对称的思想,同时由特殊到一般的思想、分类讨论的思想、数形结合的思想及方程的思想都应引起广泛的重视和应用.教学重点:轴对称、轴对称变换、等腰三角形的性质和判定教学难点:等腰三角形的性质和判定.掌握等腰三角形的性质和判定,并能应用这些知识是学好本章的关键.全章巩固训练:1.(-2,1)点关于x轴对称的点坐标为__________.2.△ABC中,AB边上的中线CD将△ABC分成两个等腰三角形,则∠ACB=_______度.3.等腰三角形的顶角为x度,则一腰上的高线与底边的夹角是___________度.4.在“线段,角,半圆,长方形,梯形,三角形,等边三角形”这七个图形中,是轴对称的图形有__个.5.下列平面图形中,不是轴对称图形的是()6.下列英文字母属于轴对称图形的是()(A)N(B)S(C)H(D)K7.下列图形中对称轴最多的是()(A)圆(B)正方形(C)等腰三角形D)线段8.如果一个三角形两边的垂直平分线的交点在第三边上,那么这个三角形是()(A)锐角三角形.(B)直角三角形(C)钝角三角形.(D)不能确定.9.以下叙述中不正确的是()A、等边三角形的每条高线都是角平分线和中线B、有一内角为的等腰三角形是等边三角形C、等腰三角形一定是锐角三角形D、在一个三角形中,如果两条边不相等,那么它们所对的角也不相等;二次备课(A)(B)(C)(D)反之,如果两个角不相等,那么它们所对的边也不相等。10.如图,要在公路MN旁修建一个货物中转站P,分别向A、B两个开发区运货。(1)若要求货站到A、B两个开发区的距离相等,那么货站应建在那里?(2)若要求货站到A、B两个开发区的距离和最小,那么货站应建在那里?(分别在图上找出点P,并保留作图痕迹,写出相应的文字说明.)12、如图,△ABC中,边AB、BC的垂直平分线交于点O.(1)求证:PA=PB=PC.(2)点P是否也在边AC的垂直平分线上?由此你还能得出什么结论?13、如图:△ABC的边AB的延长线上有一个点D,过点D作DF⊥AC于F,交BC于E,且BD=BE,求证:△ABC为等腰三角形。教学反思:吉化三中教学设计第13次ABCDFE第(1)题图MN.A.B第(2)题图MN.A.B甲DCABFE乙DCAB课题:专项(一)课型:新课备课时间:授课时间:教学目标:知识技能过程与方法德育渗透体会全等的思想,同时由特殊到一般的思想、分类讨论的思想、数形结合的思想及方程的思想都应引起广泛的重视和应用.教学重点:全等三角形的概念及性质教学难点:常见的三种模型全等第一回:全等三角形...