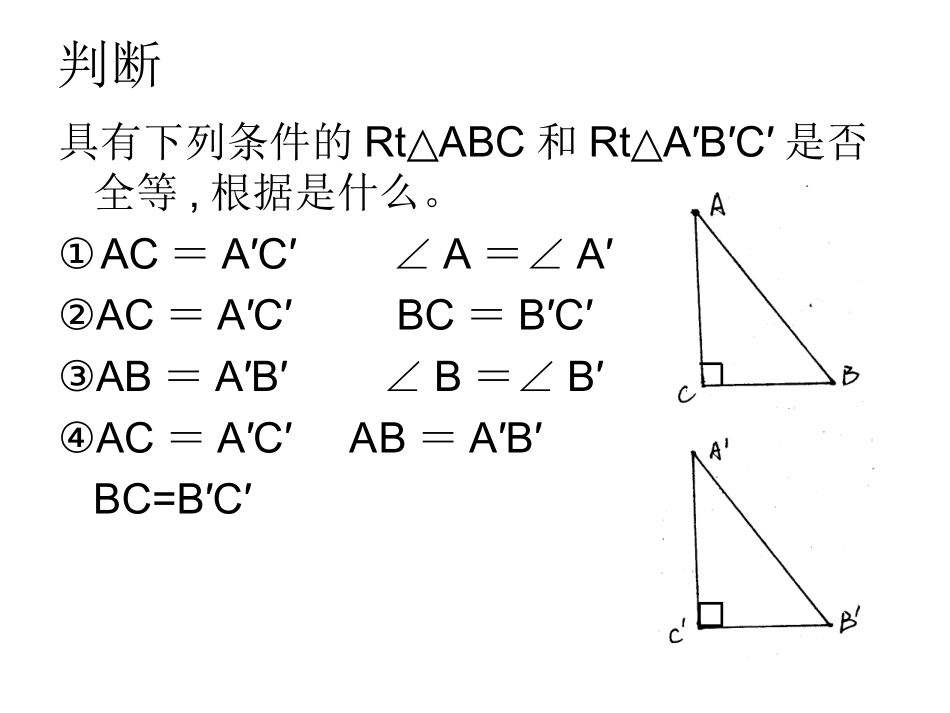
12.2.4直角三角形全等的判定方法(HL)蛟河三中刘桂霞判断具有下列条件的RtABC△和RtA′B′C′△是否全等,根据是什么。①AC=A′C′∠A=∠A′②AC=A′C′BC=B′C′③AB=A′B′∠B=∠B′④AC=A′C′AB=A′B′BC=B′C′问题:在RtABC△和RtA△´B´C´中,已知AB=A´B´,AC=A´C´则这两个三角形是什么关系?C´A´B´ABCA全等B不全等C没关系动手操作:已知RtABC,△B=90°.∠求作△A´B´C´,使∠B´=90°,AB=A´B´,AC=A´C´ABC直角三角形全等的条件AC=A´C´AB=A´B´∴RtABC△≌RtA´B´C´(HL)△斜边和一条直角边对应相等的两个直角三角形全等简写成“斜边、直角边”或“HL”.在Rt△ABC和Rt△ABC´´´中A´CBAB´C´几何语言几何语言∵∠B=B´=90∠°想一想到现在为止,你能够用几种方法说明两个直角三角形全等?答:有SAS、ASA、AAS、SSS、HL五种B'C'A'ACB例1:如图,AC⊥BC,AD⊥BDAC=BD.证明:BC=AD解:∵AC⊥BC,BD⊥AD∴∠D=∠C=90°在Rt△ABC和Rt△BAD中AB=BAAC=BD∴Rt△ABC≌Rt△BAD(HL)∴BC=ADDABC1.如图,AC=AD,∠C=∠D=90°,求证:BC=BD练习证明:C∵∠=∠D=90°∴△ABC与△ABD都是直角三角形在RtABC△与RtABD△中AB=ABAC=AD∴RtABC△≌RtABD△(HL)∴BC=BD2.如图,在△ABC中,BD=CD,DE⊥AB,DF⊥AC,E、F为垂足,DE=DF,求证:(1)△BED≌△CFD.(2)AE=AF(1)证明:∵DEAB⊥,DFAC⊥∴∠BED=CFD=90°∠在RtBED△与RtCFD△中,DE=DFBD=CD∴△BED≌CFD(HL)△证明:连接AD∵DEAB⊥,DFAC⊥∴∠AED=∠AFD=90°在Rt△AED与Rt△AFD中,AD=ADDE=DF∴Rt△AED≌Rt△AFD(HL)∴AE=AF小结本节课你有什么收获?作业1、如图∠B=∠E=90°,AB=AE,∠1=∠2,则∠3=∠4,请说明理由。2、如图,CD、C′D′分别是Rt△ABC,Rt△A′B′C斜边上的高,且CB=C′B′CD=C′D′.求证:△ABC≌△A′B′C′.