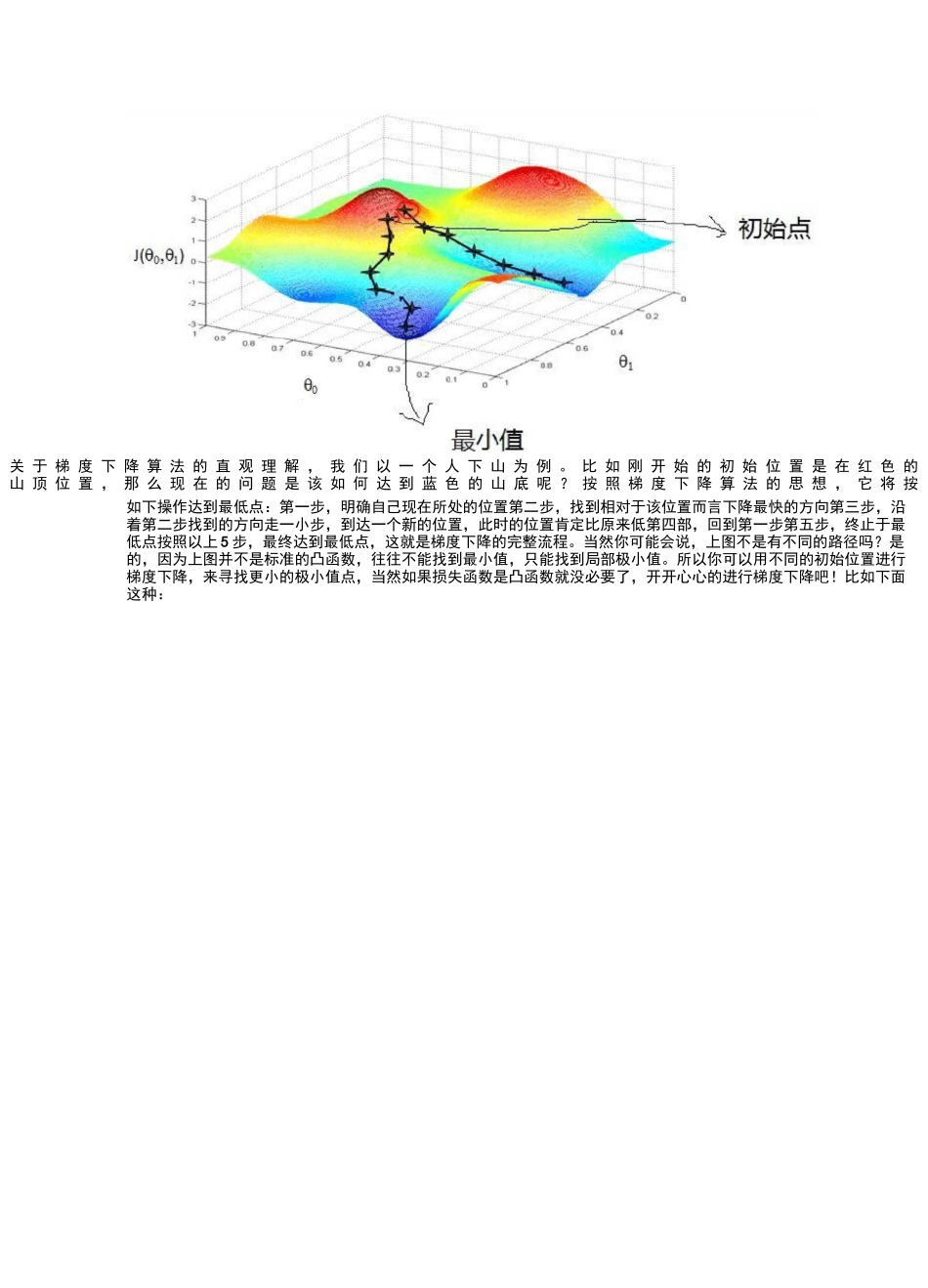
原创ICDA数据分析研究院,转载需授权介绍如果说在机器学习领域有哪个优化算法最广为认知,用途最广,非梯度下降算法莫属。梯度下降算法是一种非常经典的求极小值的算法,比如在线性回归里我们可以用最小二乘法去解析最优解,但是其中会涉及到对矩阵求逆,由于多重共线性问题的存在是很让人难受的,无论进行L1正则化的Lasso回归还是L2正则化的岭回归,其实并不让人满意,因为它们的产生是为了修复此漏洞,而不是为了提升模型效果,甚至使模型效果下降。但是换一种思路,比如用梯度下降算法去优化线性回归的损失函数,完全就可以不用考虑多重共线性带来的问题。其实不仅是线性回归,逻辑回归同样是可以用梯度下降进行优化,因为这两个算法的损失函数都是严格意义上的凸函数,即存在全局唯一极小值,较小的学习率和足够的迭代次数一定可以达到最小值附近,满足精度要求是完全没有问题的。并且随着特征数目的增多(列如100000),梯度下降的效率将远高于去解析标准方程的逆矩阵。神经网络中的后向传播算法其实就是在进行梯度下降,GDBT(梯度提升树)每增加一个弱学习器(CART回归树)近似于进行一次梯度下降,因为每一棵回归树的目的都是去拟合此时损失函数的负梯度,这也可以说明为什么GDBT往往没XGBoost的效率高,因为它没办法拟合真正的负梯度,而Xgboost的每增加的一个弱学习器是使得损失函数下降最快的解析解。总之梯度下降算法的用处十分广泛,我们有必要对它进行更加深入的理解。关于梯度下降算法的直观理解关于梯度下降算法的直观理解,我们以一个人下山为例。比如刚开始的初始位置是在红色的山顶位置,那么现在的问题是该如何达到蓝色的山底呢?按照梯度下降算法的思想,它将按如下操作达到最低点:第一步,明确自己现在所处的位置第二步,找到相对于该位置而言下降最快的方向第三步,沿着第二步找到的方向走一小步,到达一个新的位置,此时的位置肯定比原来低第四部,回到第一步第五步,终止于最低点按照以上5步,最终达到最低点,这就是梯度下降的完整流程。当然你可能会说,上图不是有不同的路径吗?是的,因为上图并不是标准的凸函数,往往不能找到最小值,只能找到局部极小值。所以你可以用不同的初始位置进行梯度下降,来寻找更小的极小值点,当然如果损失函数是凸函数就没必要了,开开心心的进行梯度下降吧!比如下面这种:1021000120卫0岂50—75问题是,如何用数学语言去描述以上5步呢?梯度下降算法的理论推导一元函数一元函数的导数我相信大家都学过,其几何意义是某点切线的斜率,除此之外它还能表示函数在该点的变化率,导数越大,说明函数在该点的变化越大。AxT坨州+xAxr血)=旳型=臥山心-皿则导函数本身则代表着函数沿着X方向的变化率二元函数对于二元函数,z=f(x,y),它对X和y的偏导数分别表示如下:函数在y方向不变的情况下,函数值沿X方向的变化率函数在X方向不变的情况下,函数值沿y方向的变化率有了以上的了解,我们分别知道了函数在单独在X和y方向上的变化率现在有一个问题,我想知道函数在其他方向上的变化率怎么办?比如下图中的u方向上:示,也就是说任意一方向上的变化,都可以分解到X和y两个方向上。比如,我想求u方向上的变化率,根据导函数的定义若:Asf(丫+cofsftjy-f-Ausinrt)—f(心lim——=hm:::::—Au—/Vniku—>0△也其中a是U方向与X正方向的夹角极限存在,可用洛必达法则,分子分母同时对求导原式等于:li叫cosrt-+打(芒裁)sina=,仁(障4-⑦y)sina令:Du=&ey)cosft-4翁(ar,y)sillQ-这是一个自变量是a的函数,我们将其命名为方向导数,其表明随着a的不同,方向不同,函数的变化率不同。至此,我们推出了,方向导数的概念,还记得我们的梯度下降算法的第二步是什么吗?”找到相对于该位置而言下降最快的方向“而我们的方向导数,本身代表的就是函数变化率与方向的关系,也就是说我们需要利用方向导数,找到使得函数变化率最大的方向那么,问题来了,在哪一个方向上变化率最大呢?寻找函数变化率最大的方向-梯度我们可以这样改写,令:一1=(丘仗崩)/护(皿讷),/'=(cosQ^inct)则:口訂匕y)=才也亍=*~te是两个向量的夹角显然,当...