二次根式的运算VIP免费

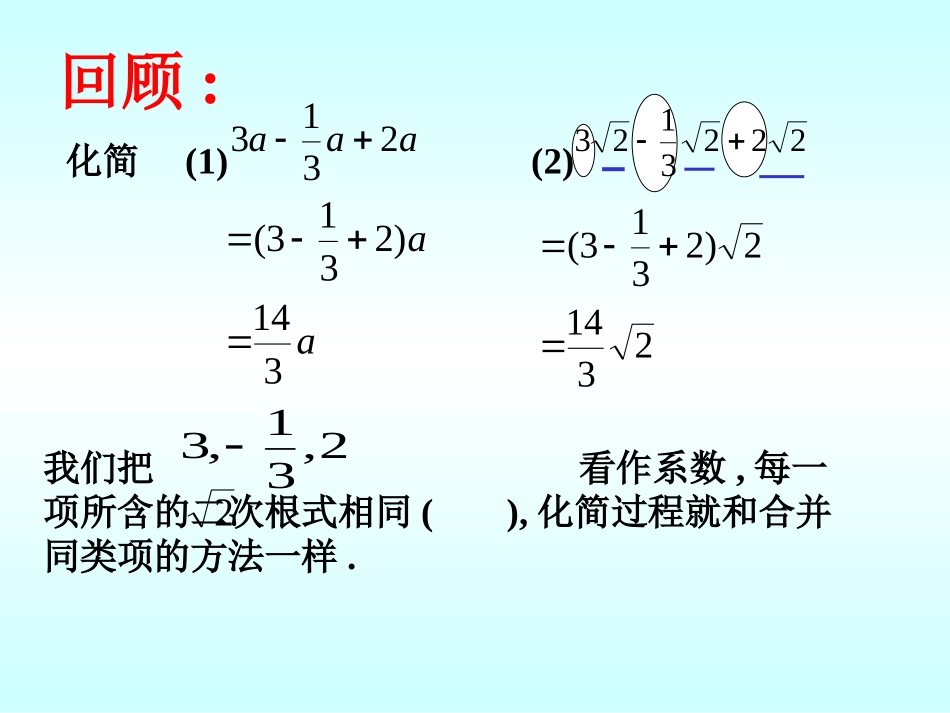
回顾:化简(1)(2)aaa2313222312323142)2313(aa314)2313(我们把看作系数,每一项所含的二次根式相同(),化简过程就和合并同类项的方法一样.2,31,323113112先化简,在求出近似值(精确到0.01).(1)例32223343332解：原式3323313273.13每一个二次根式化成最简后再合并所含有的二次根式完全相同的项.)122461(3223先化简,再求出近似值(精确到0.01).(1)练习151612511252计算(1)(2)(3)(两种算法)6)3383(例4263273)2748(注意:1.二次根式四则混合运算的顺序和整式的四则混合运算的顺序是一样的,含相同二次根式的项要合并.2.运算律同样适用于二次根式的运算.多项式的乘法法则和乘法公式同样适用于二次根式的多项式乘法.计算(1)(2)(3)例5)2233)(3322()223)(22(2)632(解:原式=22)33()22(=4×2-9×3=-19计算(1)(2)(3)2322421513)151(3)22)(21(225534练习3在RtABC△中，∠C=90°，AB=,AC=求RtABC△的周长和面积.2322ACB求当a=时,代数式(a-1)2-(a+)(a-1)的值.22的值。求已知22,23,23bababa比较大小,并说明理由.5264与052,0646410)64(210)52(25264作业本及书上作业题注意:1.二次根式四则混合运算的顺序和整式的四则混合运算的顺序是一样的,含相同二次根式的项要合并.2.运算律同样适用于二次根式的运算.3.计算结果要最简.