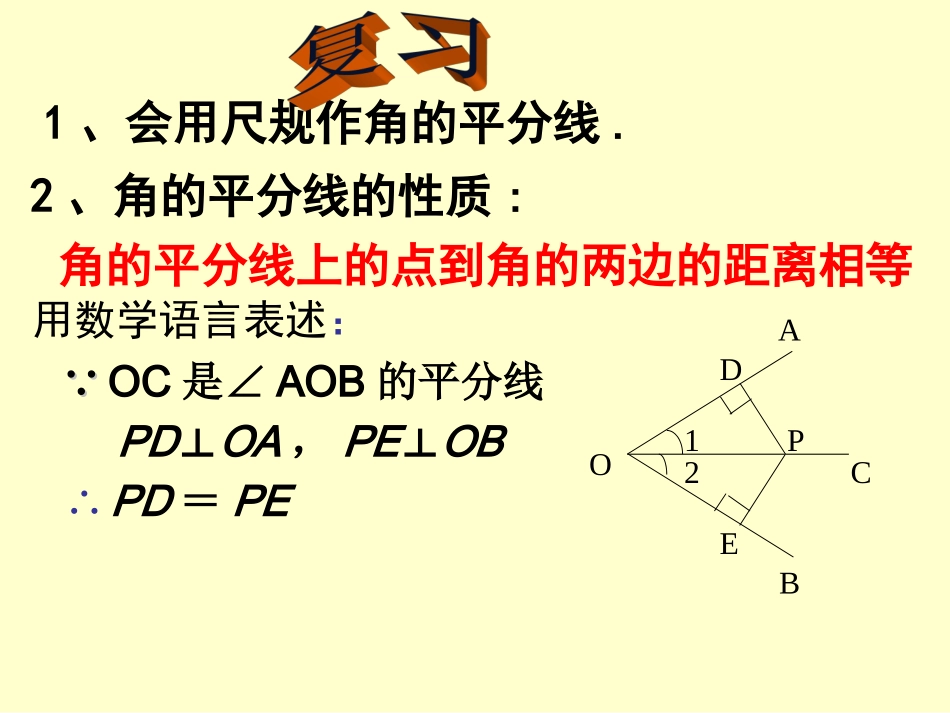
1、会用尺规作角的平分线.角的平分线上的点到角的两边的距离相等2、角的平分线的性质:OCB1A2PDEPD⊥OA,PE⊥OB∵∵OC是∠AOB的平分线∴PD=PE用数学语言表述:•反过来,到一个角的两边的距离相等的点是否一定在这个角的平分线上呢?已知:如图,QD⊥OA,QE⊥OB,点D、E为垂足,QD=QE.求证:点Q在∠AOB的平分线上.证明:∵∵QD⊥OA,QE⊥OB(已知),∴∠QDO=∠QEO=90°(垂直的定义)在Rt△QDO和Rt△QEO中QO=QO(公共边)QD=QE∴Rt△QDORt≌△QEO(HL)∴∠QOD=∠QOE∴点Q在∠AOB的平分线上已知:如图,QD⊥OA,QE⊥OB,点D、E为垂足,QD=QE.求证:点Q在∠AOB的平分线上.结论:到角的两边的距离相等的点在角的平分线上。结论:到角的两边的距离相等的点在角的平分线上。∵∵QD⊥OA,QE⊥OB,QD=QE.∴点Q在∠AOB的平分线上.用数学语言表示为:角的平分线上的点到角的两边的距离相等.∵∵QD⊥OA,QE⊥OB,点Q在∠AOB的平分线上∴QD=QE应用:要在S区建一个集贸市场,使它到公路,铁路距离相等,且离公路,铁路的交叉处500米,应建在何处?(比例尺1:20000)SO公路铁路500米=厘米根据比例尺1:20000图上应画厘米500002.5例题:在△ABC中,D是BC的中点,DE⊥AB,DF⊥AC,垂足分别是E,F,且BE=CF。求证:AD是△ABC的角平分线。ABCEFD证明:∵DEAB,DFAC⊥⊥∴∠BED=CFD=90°∠∵D是BC的中点∴BD=CD在Rt△BED和Rt△CFD中BD=CDBE=CF∴Rt△BDERt≌△CDF(HL)∴DE=DF∵DE=DF,DEAB,DFAC⊥⊥∴D点在∠BAC的平分线上即:AD是∠BAC的角平分线例2:如图,△ABC的角平分线BM,CN相交于点P,求证:点P到三边AB、BC、CA的距离相等∵BM是△ABC的角平分线,点P在BM上,ABCPMNDEF∴PD=PE(角平分线上的点到这个角的两边距离相等).同理,PE=PF.∴PD=PE=PF.即点P到三边AB、BC、CA的距离相等证明:过点P作PDAB⊥于D,PEBC⊥于E,PFAC⊥于F如图,已知△ABC的外角∠CBD和∠BCE的平分线相交于点F,求证:点F在∠DAE的平分线上.证明:过点F作FGAE⊥于G,FHAD⊥于H,FMBC⊥于MGHM∵点F在∠BCE的平分线上,FG⊥AE,FM⊥BC∴FG=FM又∵点F在∠CBD的平分线上,FH⊥AD,FM⊥BC∴FM=FH∴FG=FH∴点F在∠DAE的平分线上利用结论,解决问题练一练1、如图,为了促进当地旅游发展,某地要在三条公路围成的一块平地上修建一个度假村.要使这个度假村到三条公路的距离相等,应在何处修建?想一想在确定度假村的位置时,一定要画出三个角的平分线吗?你是怎样思考的?你是如何证明的?到角的两边的距离相等的点在角的平分线上。∵∵QD⊥OA,QE⊥OB,QD=QE.∴点Q在∠AOB的平分线上.用数学语言表示为:角的平分线上的点到角的两边的距离相等.∵∵QD⊥OA,QE⊥OB,点Q在∠AOB的平分线上∴QD=QE